Target-oriented wave-equation inversion: regularization in the reflection angle

Linear least-squares inversion

Tarantola (1987) formalizes the geophysical inverse problem. A linear version linking the reflectivity to the data has being discuss in the literature (Nemeth et al., 1999; Clapp, 2005; Kuhl and Sacchi, 2003). It provides a theoretical approach to compensate for experimental deficiencies (e.g., acquisition geometry, complex overburden), while being consistent with the acquired data. This approach can be summarized as follows: given a linear modeling operator 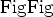${\bf L}$, compute synthetic data d using 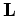${\bf d}={\bf L}{\bf m}$ where m is a reflectivity model. Given the recorded data 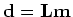${\bf d}_{obs}$, a quadratic cost function,

$$S({\bf m})=\Vert {\bf d} - {\bf d}_{obs} \Vert^2 =\Vert {\bf L}{\bf m} - {\bf d}_{obs} \Vert^2,$$ (1)

is formed. The reflectivity model 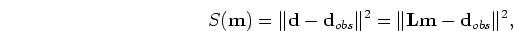$\hat{{\bf m}}$ that minimizes 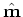$S({\bf m})$ is given by the following:

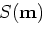$$\hat{{\bf m}}=({\bf L}'{\bf L})^{-1}{\bf L}' {\bf d}_{obs} = {\bf H}^{-1} {\bf m}_{mig},$$ (2)

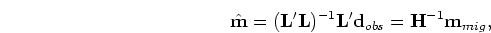where ${\bf L}'$ (migration operator) is the adjoint of the linear modeling operator 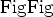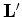${\bf L}$, ${\bf m}_{mig}$ is the migration image, and 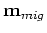${\bf H}={\bf L}'{\bf L}$ is the Hessian of $S({\bf m})$.

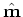The main difficulty with this approach is the explicit calculation of the inverse Hessian. In practice, it is more feasible to compute the least-squares inverse image as the solution of the linear system,

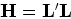$${\bf H} \hat{{\bf m}}={\bf m}_{mig},$$ (3)

by using an iterative inversion algorithm.

Target-oriented wave-equation inversion: regularization in the reflection angle