




Next: About this document ...
Up: Jousselin and Biondi: Anisotropic
Previous: REFERENCES
In anisotropic wave propagation
the phase angles and velocities are different
from the group angles and velocities.
In this appendix we briefly review the concepts of phase and group
angles and velocities and the relationships between these
physical quantities.
The transformation
from phase velocity  to group velocity V
is conventionally defined as the following
Tsvankin (2001):
to group velocity V
is conventionally defined as the following
Tsvankin (2001):
| 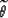 |
(10) |
where 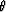 is the phase propagation angle.
The associated transformation from phase angles
to group angles
is the phase propagation angle.
The associated transformation from phase angles
to group angles  is defined
as:
is defined
as:
| 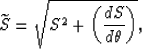 |
(11) |
Dellinger and Muir (1985) propose,
and heuristically motivate,
the following symmetric relations for the inverse transforms:
| 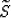 |
(12) |
where  and S are respectively the phase slowness
and the group slowness,
and
We use the heuristic relation in equation 13
to derive some of the analytical results presented in this paper.
Furthermore, we use all the above relationships
to compute the kinematic numerical results presented
in this paper.
and S are respectively the phase slowness
and the group slowness,
and
We use the heuristic relation in equation 13
to derive some of the analytical results presented in this paper.
Furthermore, we use all the above relationships
to compute the kinematic numerical results presented
in this paper.





Next: About this document ...
Up: Jousselin and Biondi: Anisotropic
Previous: REFERENCES
Stanford Exploration Project
5/6/2007
 to group velocity V
is conventionally defined as the following
Tsvankin (2001):
to group velocity V
is conventionally defined as the following
Tsvankin (2001):
 to group velocity V
is conventionally defined as the following
Tsvankin (2001):
to group velocity V
is conventionally defined as the following
Tsvankin (2001):
 and S are respectively the phase slowness
and the group slowness,
and
and S are respectively the phase slowness
and the group slowness,
and