Use of ADCIGs

There are many events in data space that migrate to the same point in image space (if the migration velocity is perfect), but with different opening angles. In the class of events discussed above, because of limited recording geometries we do not expect to model all those angles. However, if we can capture some subset of angles, we can make use of the ADCIGs to infill these missing angles and generate a more complete multiple model. When migration velocity is same as the multiple velocity, this reduces to simple interpolation or extrapolation, because events will be perfectly flat in the ADCIGs. In cases of imperfect velocity, Radon-style transforms can be used to accomplish the same goal.

To illustrate the point, I extract an ADCIG corresponding to a surface location of 8000 ft (where the dipping multiple persists). Figure (a) is the ADCIG of the recorded data and shows angles at which the multiple is actually illuminated. Figure (b) displays the illumination range of the modeled multiple. Note that the modeled multiple is missing at far angles where the recorded multiple exists. This indicates that SRMP in this case was unable to model far angles. Figure (c) is the ADCIG for the data obtained after removing the multiple model generated using SRMP (data space removal). Again, we were able to get rid of multiple energy close to zero offset, but we still have multiple energy at far offsets.

 

ADCIG
Figure 7 ADCIGs for (a) complete data (b) multiple model and (c) data after removing the multiple model

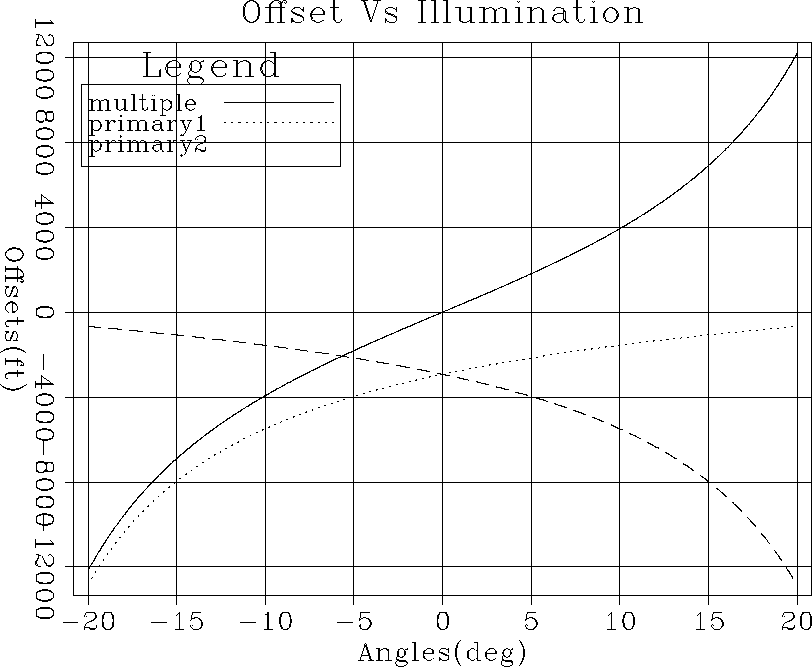
For a given velocity model and recording geometry, we can analytically compute the angles up to which we will be able to model a particular multiple, and the angles up to which it will be actually recorded. The multiple event DD maps as a dipping reflector with twice the dip in image space. ADCIGs above also show the angular illumination for this multiple event. Figure shows a plot between illumination angle and offsets for an image point located at the multiple event, with twice the dip of the original and having an X position of 8000 ft. The plot shows the relation between surface offsets and illumination angles for the first-order multiple event DD along with the two primaries that contribute towards it. It can be noticed from the plot that if we limit our recording from -4000 ft to 4000 ft, the multiple will be illuminated from -10 to +10 degrees. To model this multiple we need to record both the primaries that contribute towards it. The plot shows that for limited offsets we record both primaries only in an angular range of -5 to +5 degrees. This would be the range in which we will be able to model the multiple, which reiterates the inability of SRMP to model multiples at far opening angles, with such geometries and limited offsets.

 

angoff Figure 8 The relation between recording offsets and opening angles for the multiple event with several bounces on the dipping layer, and the primaries that contribute to it, for an image point corresponding to the X position of 8000 ft.

To obtain Figure (c) we constructed the multiple model in the data space, removed it from the data and then migrated it to image space and constructed ADCIGs. Equivalently, this process could have been carried out in image space, in which case we would migrate the data and the multiple model independently to the image space and then do the subtraction.