




Next: Finite Difference Stencils by
Up: Etgen: Time domain finite-difference
Previous: Etgen: Time domain finite-difference
All finite-difference solutions to wave equations in media with more than one spatial dimension have numerical phase and group velocities
that differ from the desired phase and group velocities of the "true" solution.
The errors manifest themselves as "dispersion"; different frequencies propagate at different speeds.
This leads to progressively greater distortion of the propagating waveforms with increasing time and
propagation distance.
For example, the standard second-order in time,
second-order in space finite-difference approximation to the 2D or 3D acoustic wave equation needs a large
degree of oversampling of the spatial axes (ten points per wavelength or more) to achieve remotely reasonable accuracy.
Thus, despite its simplicity, it's almost never used in practice.
Finite difference methods that use spatial difference operators with more points, so called high-order finite-difference methods
Dablain (1986); Etgen (1986, 1988),
are commonly used to improve the accuracy and efficiency of
the method, as well as reduce its memory requirements, which is particularly important in 3D Wu et al. (1996).
Most original high-order finite-difference methods used a Taylor-series approach to derive spatial difference coefficients, while
employing second-order differences in time to preserve the simplicity of a 3-point time marching scheme.
Dablain (1986) is probably the earliest, most thorough description of this method. In the same paper, Dablain showed how to
create a time marching algorithm that has fourth-order accuracy in time by applying the spatial difference operator
in a two-term cascade and weighting the terms of the cascade appropriately to cancel the leading order error of the time discretization.
The ultimate quest for accuracy often combines higher-order time expansion with
the Fourier pseudo-spectral method Reshef et al. (1988) for the spatial derivatives.
That approach can be generalized to many
terms, ultimately leading to orthogonal-polynomial series solutions that have spectral accuracy Tal-Ezer et al. (1987).
The complexity involved in implementing these "very accurate" methods means that they don't see much large-scale practical application,
particularly for reverse-time migration.
They are also difficult to implement as "out-of-core" solutions or on a cluster of machines using message passing;
techniques that are often necessary for large 3D problems.
So, we return to the finite-difference method in the hope of creating an accurate scheme that is
computationally flexible and efficient.
Difference operators derived from Taylor-series expansion are "conservatve" in that they have very high accuracy for low wavenumbers,
but in achieving that, they waste some potential accuracy improvements at higher wavenumbers.
In a classic paper, Holberg (1987) shows how to
find improved spatial difference operators using optimization techniques. Most modern high-order finite-difference techniques use his method
to create spatial-difference coefficients. But I believe there are a couple of fundamental short-comings in Holberg's design; so I revisited the
design problem for optimum finite-difference schemes.
In one space dimension, the accuracy of the second-order in time, second-order in space finite-difference method improves the closer the
time step size is to the stability limit, 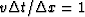 .It's an interesting curiosity
that the two sources of error
cancel exactly when taking the time-step size at exactly the stability limit.
While this exact cancellation does not exist for the second-order finite-difference method in any higher number of spatial dimensions, it does
point out that there is an opportunity to "tune" the spatial-difference coefficient design by trading it off against the errors generated by
the time discretization.
I also felt that the classical "equiripple" filter design technique that Holberg used leads to unacceptably large errors at low and moderate
wavenumbers, paricularly when using relatively compact difference operators.
.It's an interesting curiosity
that the two sources of error
cancel exactly when taking the time-step size at exactly the stability limit.
While this exact cancellation does not exist for the second-order finite-difference method in any higher number of spatial dimensions, it does
point out that there is an opportunity to "tune" the spatial-difference coefficient design by trading it off against the errors generated by
the time discretization.
I also felt that the classical "equiripple" filter design technique that Holberg used leads to unacceptably large errors at low and moderate
wavenumbers, paricularly when using relatively compact difference operators.





Next: Finite Difference Stencils by
Up: Etgen: Time domain finite-difference
Previous: Etgen: Time domain finite-difference
Stanford Exploration Project
5/6/2007