




Next: Numerical examples
Up: Shan et al.: Plane-wave
Previous: Practice considerations
It is well known that a VTI (transversely isotropic with a vertical symmetry axis) medium is circularly symmetric in the horizontal plane.
Therefore, the medium is still VTI after rotating the azimuth of the model (equation 18).
In the second rotation step (equation 19), a VTI medium in Cartesian coordinates changes
to a TTI (tilted TI) medium with a constant tilting angle 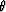 in the new coordinates.
We keep the y2-axis in (x,y) plane
when we rotate the coordinates. This guarantees the symmetry axis of the new TTI media in the new
plane (x2,z2). For this kind of TTI media, the dispersion relation is not symmetric in the in-line direction
but it is symmetric in the cross-line direction in the new coordinates. The
extrapolation operator for this kind of TTI media is simpler than the general TTI media.
We need a wavefield-extrapolation operator for TTI media to apply plane-wave migration in tilted
coordinates in VTI media. We use optimized implicit finite-difference methods for TTI media Shan (2006a). The coefficients for the finite-difference scheme are obtained by
fitting the dispersion relation with rational functions.
in the new coordinates.
We keep the y2-axis in (x,y) plane
when we rotate the coordinates. This guarantees the symmetry axis of the new TTI media in the new
plane (x2,z2). For this kind of TTI media, the dispersion relation is not symmetric in the in-line direction
but it is symmetric in the cross-line direction in the new coordinates. The
extrapolation operator for this kind of TTI media is simpler than the general TTI media.
We need a wavefield-extrapolation operator for TTI media to apply plane-wave migration in tilted
coordinates in VTI media. We use optimized implicit finite-difference methods for TTI media Shan (2006a). The coefficients for the finite-difference scheme are obtained by
fitting the dispersion relation with rational functions.





Next: Numerical examples
Up: Shan et al.: Plane-wave
Previous: Practice considerations
Stanford Exploration Project
5/6/2007