Regularization in the prestack image space

The previous subsection solve equation 3 in a poststack image domain (zero subsurface-offset). But a prestack regularization is necessary to reduce the noise in the inversion result. If subsurface offset is included in the computation of the Hessian, a generalization to the prestack image domain of equation 4 is possible.

Three different regularization schemes for wave-equation inversion have been discussed in the literature. First, an identity operator which is customary in many scientific applications (damping). Second, a geophysical regularization which penalizes the roughness of the image in the offset ray parameter dimension (which is equivalent the reflection angle dimension) Kuehl and Sacchi (2001); Prucha et al. (2000). Third, a differential semblance operator to penalize the energy in the image not focused at zero subsurface-offset Shen et al. (2003). In this paper I use the third regularization scheme, the regularization in the reflection angle domain.

A generalization to the prestack image domain of equation 3 needs regularization to obtain a stable solution. The first option for regularization is a customary damping that can be stated as follows:

$$\begin{eqnarray} {\bf H}({\bf x, h};{\bf x',h'}) \hat{{\bf m}}({\bf x},{\bf h})-... ...\ \varepsilon{\bf I}\hat{{\bf m}}({\bf x},{\bf h})&\approx&0, \end{eqnarray}$$ (5)

where ${\bf x}=(z,x,y)$ is a point in the image, and ${\bf h}=(h_x,h_y,h_z)$ is the half subsurface-offset. The subsurface-offset Hessian ${\bf H}({\bf x, h};{\bf x',h'})$ is

$$\begin{eqnarray} {\bf H}({\bf x,h};{\bf x',h'})=\sum_{\omega} \sum_{{\bf x}_s} ... ...{\bf x}_r;\omega) {\bf G}({\bf x'-h'},{\bf x}_r;\omega),\nonumber \end{eqnarray}$$

where ${\bf G}({\bf x},{\bf x}_s;\omega)$ and ${\bf G}({\bf x},{\bf x}_r;\omega)$ are the Green functions from shot position ${\bf x}_s$ and receiver position ${\bf x}_r$ to a model space point ${\bf x}$.

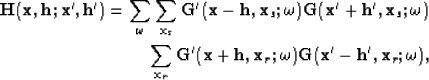The third regularization option for the prestack generalization of equation 3, is penalizing the energy in the image not focused at zero subsurface-offset. This is obtained using the fitting goals,

$$\begin{eqnarray} {\bf H}({\bf x, h};{\bf x',h'}) \hat{{\bf m}}({\bf x},{\bf h})-... ...\varepsilon{\bf P_h} \hat{{\bf m}}({\bf x},{\bf h})&\approx& 0, \end{eqnarray}$$ (6)

where ${\bf P_h= \vert h\vert}$ is the differential semblance operator Shen et al. (2003). The only difference between equations 5 and 6 is in the regularization operator.

In the next section I compare the numerical solution of the inversion problems stated in equations 5 and 6 to the imaging of Sigsbee model.