![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
I obtain parametric equations for migrating an impulse recorded at time tD,
data-midpoint mD, and data surface-offset hD as follows:
,
I obtain parametric equations for migrating an impulse recorded at time tD,
data-midpoint mD, and data surface-offset hD as follows:
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) in order to obtain the parametric equations for migration on a constant
velocity medium.
in order to obtain the parametric equations for migration on a constant
velocity medium.
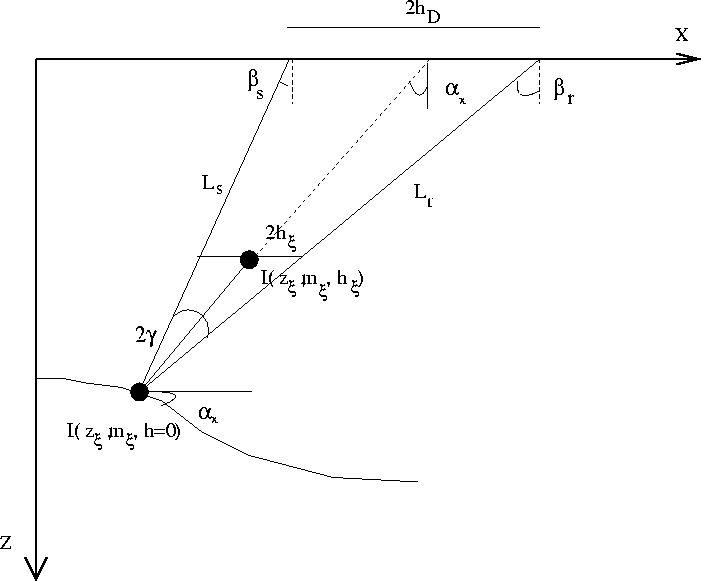
Following the derivation of Fomel (1996) and
Fomel and Prucha (1999),
and applying simple trigonometry and geometry to Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
I obtain parametric equations for migrating an impulse recorded at time tD,
data-midpoint mD, and data surface-offset hD as follows:
,
I obtain parametric equations for migrating an impulse recorded at time tD,
data-midpoint mD, and data surface-offset hD as follows:
 |
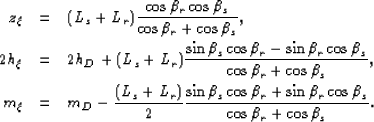 |
||
| (79) |
where the total path length is:
| (80) |
From that system of equations, Biondi (2005) shows that the total path length is
| (81) |
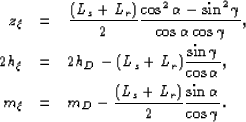 |
||
| (82) |
where ![]() and
and ![]() follow the same definition as in equation
follow the same definition as in equation ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The total path length, L, in terms of the angles
.
The total path length, L, in terms of the angles ![]() and
and ![]() is:
is:
| (83) |