f-k log-stretch PS-AMO

Next: Impulse response Up: PS Azimuth Moveout Previous: PS Azimuth Moveout

f-k log-stretch PS-AMO

The PS-DMO operator in the f-k log-stretch domain, discussed in Chapter 2, is easily extended to 3-D, and it is the basis to build the f-k log-stretch PS-AMO operator. By performing PS-DMO in the frequency-wavenumber log-stretch domain in cascade with its inverse, the PS-AMO operator is computationally efficient. This PS-AMO operator consists of two main operations. In the first operation, the input data, $P(t,{\bf x},{\bf h_1})$ , is transformed to the wavenumber domain ( $P(t,{\bf k},{\bf h_1})$ ) using FFT. Then, a lateral-shift correction is applied using the transformation vectors ( $\bf D_{10}$ and $\bf D_{02}$ ) as follows:

$\begin{displaymath} \widetilde P(t,{\bf k},{\bf h_1}) = P(t,{\bf k},{\bf h_1}) e^{i{\bf k}\cdot({\bf D_{10}} - {\bf D_{02}})}. \end{displaymath}$ (40)

The final step of the first operation is to apply a log-stretch along the time axis with the following relation:

$\begin{displaymath} \tau = \ln \left ( \frac{t}{t_c} \right ), \end{displaymath}$ (41)

where t_c is the minimum cutoff time, introduced to avoid taking the logarithm of zero. Therefore, the dataset after the first operation is $\widetilde P(\tau,{\bf k},{\bf h_1})$ . In the second operation, the log-stretched time domain ( $\tau$ ) section is transformed into the frequency domain ( $\Omega$ ) using FFT. Then, the filters $F(\Omega,{\bf k},{\bf h_1})$ and $F(\Omega,{\bf k},{\bf h_2})$ are applied as follows:

$\begin{displaymath} P(\Omega,{\bf k},{\bf h_2}) = \widetilde P(\Omega,{\bf k},{\... ...c{F(\Omega,{\bf k},{\bf h_1})}{F(\Omega,{\bf k},{\bf h_2})}. \end{displaymath}$ (42)

The filter $F(\Omega,{\bf k},{\bf h_{i=(1,2)}})$ is given by

$\begin{displaymath} F(\Omega,{\bf k},{\bf h_i}) = e^{i\Phi(\Omega,{\bf k},{\bf h_i})}, \end{displaymath}$ (43)

with the phase function $\Phi(\Omega,{\bf k},{\bf h_i})$ defined by either

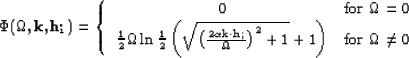$\begin{displaymath} \Phi(\Omega,{\bf k},{\bf h_i}) = \left \{ \begin{array} {cc}... ...right)} & \mbox{for $\Omega \ne 0$} \end{array} \right . \end{displaymath}$ (44)

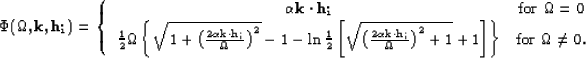$\begin{displaymath} \Phi(\Omega,{\bf k},{\bf h_i}) = \left \{ \begin{array} {cc}... ...ght \} & \mbox{for $\Omega \ne 0$}. \end{array} \right . \end{displaymath}$ (45)

To implement this PS-AMO operator, we use the following procedure:

1.: Calculate the FFT along the midpoint axis for each input offset cube.
2.: Compute the transformation vectors $\bf D_{10}$ and $\bf D_{02}$ with equations and .
3.: Apply the lateral shift of the transformation vectors as a phase shift with equation .
4.: Perform the log-stretch transformation over the time axis using equation .
5.: Calculate the FFT along the transformed time axis.
6.: Compute the filters $F(\Omega,{\bf k},{\bf h_1})$ and $F(\Omega,{\bf k},{\bf h_2})$ .
7.: Apply these filters to the data in the log-stretch frequency-wavenumber domain with equation .
8.: Perform inverse FFT and inverse log-stretch.

The lateral shift correction, third step on the above procedure, involves a forward and inverse 2-D Fourier transform on both the inline and crossline CMP axes. Therefore, this step increases condirebly the cost of the PS-AMO operator compared with the conventional log-stetch implementation of the single mode AMO operator.

Next: Impulse response Up: PS Azimuth Moveout Previous: PS Azimuth Moveout

Stanford Exploration Project
12/14/2006