Results for first model

The non-interaction approximation is particularly simple for the first model since $\nu_0 = 0.0$. Then, (3) and (2) show that  

$$\frac{G_0}{G_{NI}} = \frac{K_0}{K_{NI}} = 1 + \rho\frac{16}{9},$$ (19)

and, therefore, we also have $\nu_{NI} = 0.0$ for all $\rho$ in this approximation -- since the proportionality between the bulk and shear moduli never changes for this case. Background bulk modulus for this model is K₀ = 4.583 GPa and corresponding shear modulus is G₀ = 6.875 GPa. In the Sayers and Kachanov (1991) scheme, $\eta_1(0) = 0.0$ GPa^-1 and $\eta_2(0) = 0.1941$ GPa^-1. All off-diagonal perturbations of the compliance matrix comes from $\eta_1$, so there is no change to the zero values off the diagonal for this case. For a single crack per grain and crack density $\rho$, all perturbations are of the form $\Delta = 2\rho\eta_2(0)$ and these perturbations are contributing only to these three compliance values: S₃₃, S₄₄ and S₅₅. The compliance matrix may next be inverted to produce the perturbed stiffness matrix, and then these values are used in the formulas in Appendix A and also in the Figures.

Without fitting

 

Fig2
Figure 2 Estimates (SC, NI, and DS) and possible bounds; (R, HS^-, HS⁺, V) on inverse shear modulus estimators G^-1_VRH of 33 examples from the numerical experiments of Grechka and Kachanov. Background medium has Poisson's ratio $\nu_0 = 0.0$ for this example. Crack density $\rho = na^3$, where n = number of penny-shaped cracks per unit volume, and a is the radius of the cracks. (If the cracks are not all the same size, then the product na³ is the appropriate average quantity.) Crack aspect ratio is assumed small, but nonzero. The estimates of individual (cracked) grain behavior as crack density increases make use of crack-influence parameters $\eta_1 = 0.0$ GPa^-1 and $\eta_2 = 0.194448$ GPa^-1 (Sayers and Kachanov, 1991) determined using the DS estimator for small crack densities. Similarly, for the NI estimator: $\eta_1 = 0.0$ GPa^-1 and $\eta_2 = 0.1941$ GPa^-1. Also note that the estimates and bounds are all consistently high (for G^-1) compared to the numerical data (x). Polycrystal bounds and estimates were obtained here without any fitting parameters, using only the very low crack density coefficients, $\eta_1$ and $\eta_2$.

 

Fig3 Figure 3 Same as Figure 2, showing corresponding results for the inverse bulk modulus estimators K-1VRH . Polycrystal bounds and estimates were also obtained here without any fitting parameters, using only the very low crack density coefficients. Note that the estimates and possible bounds are considerably higher here in relation to the numerical data (x) than in Figure 2 for the inverse shear modulus. We interpret this difference as being a result of shorter range interactions for shear, and longer range interactions for bulk modulus that are not properly taken into account by the present (overly simple) model.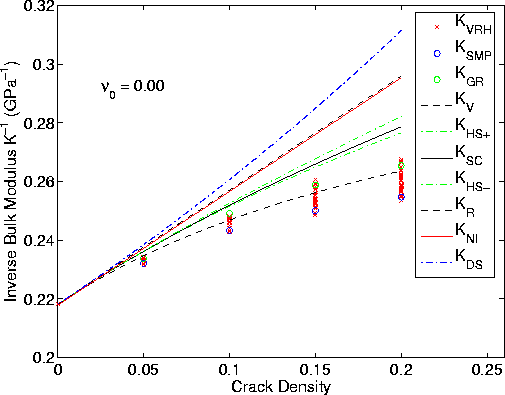

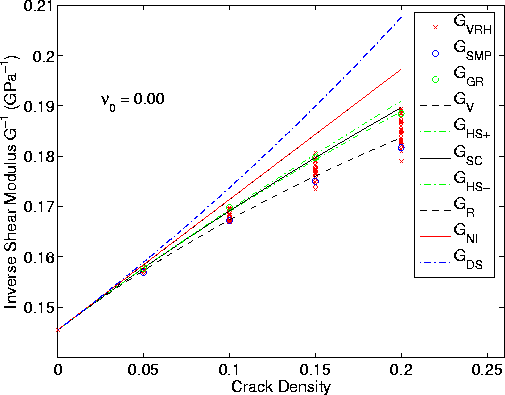
Figures 2 and 3 show the results for the first model using only the results of the NIA as input to the polycrystal of cracked-grains model. For comparison, we also display the NIA results, the differential scheme (DS) effective medium theory results (Zimmerman, 1991; Berryman, 2002), and the numerical data (x). The numerical data were actually stiffness matrices, so these matrices have been converted to Voigt-Reuss-Hill (VRH) estimates of shear and bulk moduli for plotting and comparison purposes. All curves converge at low crack densities as they should. We see that the numerical data deviate from the NIA curve substantially for both shear and bulk moduli. But the deviations are especially strong for the bulk modulus estimates. Without fitting, the shear modulus estimates have values that are about equal to the self-consistent polycrystal estimates, or higher (note the plots are inverse moduli). In contrast, the bulk modulus (inverse modulus) estimates are always significantly higher (lower) than the self-consistent estimates. We interpret this difference between the shear modulus and bulk modulus results as being due to the presence of longer range interactions for bulk modulus effects, and shorter range interactions for shear modulus effects. Thus, even without any attempt at fitting, the polycrystal grain model appears to be a fairly good model for the shear behavior, but not as good for the bulk (hydrostatic) behavior.

We can modify the results for the polycrystals of cracked-grains model by including higher order corrections from the Sayers and Kachanov (1991) model, as in the discussion accompanying Eqs. (38)-(41), and that is what we do next.

With fitting

 

Fig4 Figure 4 Same as Figure 2, but the values of 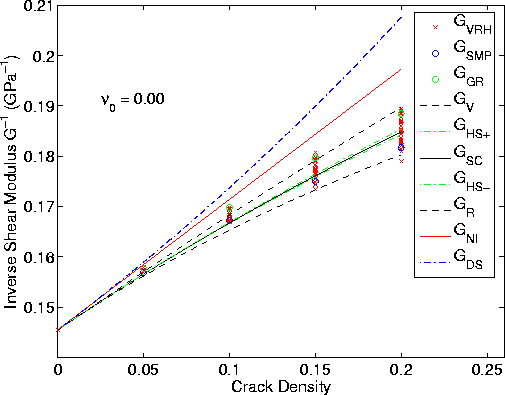$\eta_1$and $\eta_2$were obtained from an average of the shear modulus data (x) at $\rho = 0.05$.Furthermore, a quadratic correction is added to compliance values S33, S44, and S55 to give the best fit both here and simultaneously in Figure 5. Note that the spread in the data is comparable to the difference in the Reuss and Voigt bounds, but substantially greater than the spread in the HS bounds.

 

Fig5 Figure 5 Same as Figure 4, for the inverse bulk modulus. Note that the data mostly fall between the Reuss and Voigt bounds, but definitely are not close to being restricted to lie inside the HS bounds.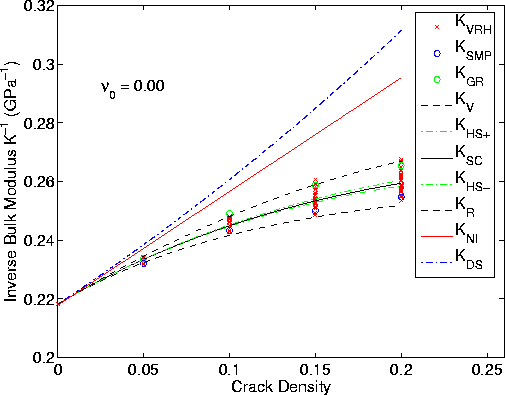

When developing our approach to fitting the numerical the data, we took the basic model of Sayers and Kachanov (1991), including the higher order corrections in powers of crack density, as discussed in Appendix B, and then tried to find the simplest set of coefficients that would fit the numerical data. Since the fit was already fairly good for shear modulus of the first model, and since it was mostly the bulk modulus that deviated very much from the numerical data, we determined that a method producing as little change as possible in the shear modulus, while still affecting the needed changes in bulk modulus, was what was needed.

Since $\eta_1 = 0.0$ for this case, $\eta_4 = 0.0$ also seemed the logical choice for this parameter. This leaves us with two crack-influence parameters to fit: $\eta_3$ and $\eta_5$. One type of increment that produces relatively small changes in shear modulus, while also changing bulk modulus, is one of the form $\Delta_{33} = 2(\eta_3 + \eta_5)\rho^2$added to S₃₃, while at the same time adding corrections $\Delta_{44} = \Delta_{55} = -2\Delta_{33}/3$to S₄₄ and S₅₅. This type of shift causes no change in the Reuss average for shear modulus. (In fact, we actually used this approach for the quadratic corrections in the second model, as will be seen in the subsequent discussion.) Although we tried this approach here, it did not seem to be as successful as desired at improving the fit to the numerical data. In particular, since the shear modulus agreement in this case could stand some improvement anyway, we modified this approach slightly and found (after some trial and error) that setting $\Delta_{44} = \Delta_{55} = 2\eta_5\rho^2 = -\Delta_{33}/3$worked better in this case. This choice does not leave the Reuss average of shear modulus unchanged, but that was not an absolute condition we needed or wanted to impose. By choosing $\Delta_{33} = -0.00275(\rho/0.05)^2/2$,we thus obtained the agreement seen in Figures 4 and 5, and no further searching for better fits to the data were pursued. These corrections are translated into numerical values for $\eta_3$ and $\eta_5$ in TABLE 1.