Solving the Forward Modeling Problem

A key development in frequency-domain waveform inversion methodology would be establishing a more rapid, yet accurate, forward modeling approach for generating Helmholtz equation solutions. This is important because, for each non-linear iteration and frequency, forward modeling is required (at least) three times: i) forward-propagating wavefield P_s to generate data 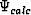$\Psi_{calc}$; ii) back-projecting wavefield residuals P_r; and iii) calculating step length 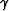$\gamma$. In this study, I solve the forward modeling problem using more efficient, though less accurate, one-way extrapolation operators. The central supposition is that the lower accuracy associated with one-way operators will be more than offset by efficiency gains and lower memory requirements of finding waveform inversion solutions. A more fundamental question is whether one-way operators are sufficiently accurate to permit waveform inversion. Demonstrating this assumption's validity is a key result of this paper.

One useful strategy for developing effective one-way operators is to consider propagation in a coordinate system geometry other than Cartesian. For example, one can specify a sideways-tilted, ray-like mesh where the extrapolation axis is predominately oriented in the direction of turning-wave propagation. In this reference frame, the bulk of wavefield continuation occurs at low angles to the extrapolation axis where one-way operators remain accurate. Wavefield propagation on non-Cartesian grids falls under the purview of RWE, which incorporates mesh geometry directly into the Helmholtz equation through additional spatially varying coefficients. The differential geometry used to describe coordinate system transformations in general space is presented in Appendix A, while the operators used in the one-way RWE approach are developed in Appendix B.

Figure 2 illustrates the geometric transformation between Cartesian (two left panels) and RWE domains (two right panels). The upper left panel shows a coordinate system mesh overlying part of the Pluto velocity model. The upper right panel shows this mesh unfolded to form a regular grid, underlying which is the interpolated velocity profile.

 

FMexample
Figure 2 Illustration of the waveform inversion forward modeling approach. The left (right) panels represent the Cartesian (Riemannian) viewpoint. Upper left: Pluto velocity profile overlain by a dipolar coordinate system mesh. Upper right: Unstretched coordinate system from upper left panel underlain by the interpolated velocity profile. Lower right: Four superimposed broadband wavefields (at 1.0s, 2.2s, 3.4s, and 4.6s) propagated through the velocity model in the upper right. Lower left: Wavefields from the lower right interpolated to Cartesian.

(The RWE coefficients in Appendix B describe the stretching effects generated by this transformation.) The bottom right panel shows four superimposed wavefield snapshots (at 1.0s, 2.2s, 3.4s and 4.6s) for a point source propagated outward from the left side of the model. Note that while some energy is lost - for example, at boundaries and steeply dipping energy - the bulk of the wavefield is extrapolated at low angles through the model. The bottom left panel shows the wavefield from the bottom right interpolated back to a Cartesian mesh. The rapid near-horizontal advancement of the wavefield through the salt is evident, as are the top-salt reflections arriving at the free surface.

The remainder of this section describes how I perform forward modeling using RWE operators. I present the rationale for using a dipolar coordinate system, detail an approximate approach for incorporating source radiation patterns and free-surface reflections, and describe a wavefield injection approach to back-propagate wavefield residuals.

 

• Dipole Coordinates
• Radiation Patterns and Free-surface
• Forward modeling examples
• Back-projection by wavefield injection