




Next: Real Data Examples
Up: Witten and Grant: Convex
Previous: Least-Squares Dix Equation
A problem is a convex optimization problem if it has the form
| 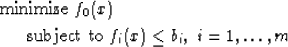 |
|
| (3) |
where 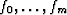 and
and 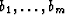 are convex functions and x exists in a convex
set,
are convex functions and x exists in a convex
set,  Boyd and Vandenberghe (2004). Convex optimization problems have many
attractive features including the guarantee of local minima to be
global and strong optimality, feasibility, and
sensitivity information. As well, there are reliable and efficient numerical
algorithms to solve these problems. Since this Dix formulation is a
least-squares problem, which is
already convex, it seems natural to try convex optimization techniques
to find the solution.
Boyd and Vandenberghe (2004). Convex optimization problems have many
attractive features including the guarantee of local minima to be
global and strong optimality, feasibility, and
sensitivity information. As well, there are reliable and efficient numerical
algorithms to solve these problems. Since this Dix formulation is a
least-squares problem, which is
already convex, it seems natural to try convex optimization techniques
to find the solution.
The data fitting goal, equation (1), can be rewritten in optimization
notation as
| 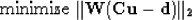 |
(4) |
where 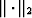 means the least-squares norm. When necessary
regularization terms are added the full set of goals, equation (2) becomes
means the least-squares norm. When necessary
regularization terms are added the full set of goals, equation (2) becomes
| 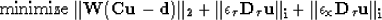 |
(5) |
in optimization notation. If i is 2 then an 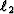 regularization is used and a smooth
model is obtained. If i is 1 then an
regularization is used and a smooth
model is obtained. If i is 1 then an 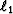 regularization
is used and the result is a blocky model, instead.
regularization
is used and the result is a blocky model, instead.
Even after inversion, there may be points in the model
space which do not make geological sense, usually due to picking
errors caused by poor resolution. Convex optimization allows for bound constraints to be
imposed on the solution, which can correct for such inconsistencies.
If we constrain the solution then we have
| 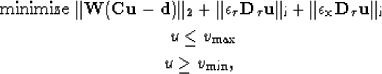 |
|
| |
| (6) |
where 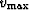 and
and 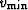 are the square of the
maximum and minimum allowable velocity models, respectively.
are the square of the
maximum and minimum allowable velocity models, respectively.
To do the convex optimization,  Grant et al. (2006) will be
used.
Grant et al. (2006) will be
used.  is a MATLAB based system for solving convex optimization
problems. It allows constraints and objectives to be specified with
common MATLAB syntax.
is a MATLAB based system for solving convex optimization
problems. It allows constraints and objectives to be specified with
common MATLAB syntax.





Next: Real Data Examples
Up: Witten and Grant: Convex
Previous: Least-Squares Dix Equation
Stanford Exploration Project
1/16/2007
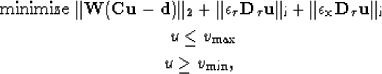
![]() Grant et al. (2006) will be
used.
Grant et al. (2006) will be
used. ![]() is a MATLAB based system for solving convex optimization
problems. It allows constraints and objectives to be specified with
common MATLAB syntax.
is a MATLAB based system for solving convex optimization
problems. It allows constraints and objectives to be specified with
common MATLAB syntax.