Gaussian Pyramid Interpolation

In this section I show how the Gaussian pyramid structure can be used to perform missing data interpolation. Consider the image on the upper leftmost side of Figure .This image has a 30 point hole in it. Now as the Gaussian pyramid structure for this image is generated both the image dimension as well as the size of the hole shrinks. At level 3, the hole is only 1 points long. Thus each level of the Gaussian pyramid contains information about the missing hole at different scale/size. This shrinking of the holes in the pyramid generation process gives a strategy to interpolate missing data without the use of prediction filters. Instead of using prediction filters the image is considered as a sum of patterns at many scales and restoration of the missing data is carried out at many scales as well.

If the size of the mising piece is comparable to the finest scale features of an image, then a good estimate of the unknown value at 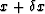$x+\delta x$ can be estimated through a simple first order linear prediction based on the first derivative of the image at the known point x as:

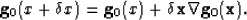$$\bold g_0(x+\delta x) = \bold g_0(x) +\bold { \delta x \nabla g_0(x)}.$$ (10)

However if the missing piece is large then more derivatives would be needed, in other words we need to examine variations at larger scales as well. An immediate analogy to this problem would be to look at the missing information itself at various scales. As the Gaussian pyramid is generated different versions of the image 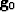$\bold g_0$ is obtained at different resolutions. The missing data in the original image is also missing at any other level of the pyramid 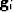$\bold g_i$, the only difference being that the scale or size of the missing piece is reduced. Thus at a coarser spatial scale we do not need to use a polynomial of high degree to fill in the missing data. At some level of the pyramid the hole would be of a size comparable to the finest scale features in that pyramid level. At this level we can use simple linear prediction to fill in the missing data. Once the missing piece is filled up at some pyramid level we can then expand, starting from that level, and wherever a missing piece of information exists we can simply use the value of the expanded level. The algorithm for the missing data interpolation would then be:

1.

Start with the initial image $\bold g_0$.

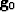2.

Form pyramid levels 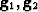$\bold g_1, \bold g_2$, and so on

3.

If at pyramid level 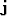$\bold j$, missing piece is very small fill 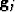$\bold g_j$ using linear prediction.

4.

Expand 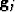$\bold g_j$ to $\bold g_{j,1}$.

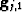5.

Fill in missing space in 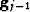$\bold g_{j-1}$ using $\bold g_{j,1}$.

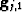6.

Expand the filled 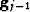$\bold g_{j-1}$ and continue filling and expanding.

7.

Finally fill in original image 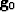$\bold g_0$ using the filled $\bold g_{1,0}$.

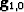8.

If needed iterate with the filled $\bold g_0$.

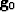9.

Stop.

This algorithm is illustrated with the dataset with the hole, shown in Figure . First the right lowermost panel of this figure is filled up using linear prediction (shown on the upper most left panel of Figure ). Starting from this filled level, expansion of the filled level followed by subsequent filling up is done till the original image is filled up (lower right panel of Figure ).