Next: Derivation of equation (30)
Up: Derivation of the derivative
Previous: Derivation of equation (26)
29)
In case of uniform scaling of velocity,
| 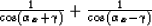 |
(46) |
The quantity 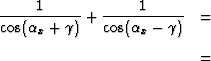 can be written
can be written
| 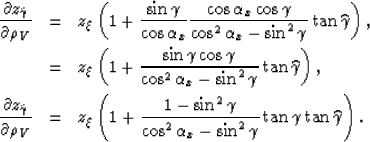 |
(47) |
| (48) |
| (49) |
| (50) |
Using equation (50), equation (46)
simplifies to
| 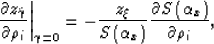 |
(51) |
| (52) |
| (53) |





Next: Derivation of equation (30)
Up: Derivation of the derivative
Previous: Derivation of equation (26)
Stanford Exploration Project
4/6/2006
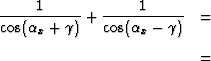 can be written
can be written