




Next: About this document ...
Up: Berryman: Seismic waves in
Previous: Shallow example
Sayers and Kachanov (1991) introduced a convenient method of analyzing
fractured (but otherwise) elastic systems. I showed here that their
method can be successfully generalized to fluid-saturated fractures.
Furthermore,
when their method is used in conjunction with Thomsen's anisotropy
parameters (Thomsen, 1986), we find not only analytical results that
aid our intuition about these complex problems, but also a means to
deconstruct velocity data and then to interpret the nature
(approximate crack density) of fractures in the system being studied.
The magnitudes of the parameters 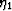 and
and 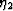 can be
determined in a straightforward way using any effective medium theory
we trust (Kachanov, 1994; Prat and Ba
can be
determined in a straightforward way using any effective medium theory
we trust (Kachanov, 1994; Prat and Ba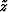 ant, 1997; Grechka, 2005);
and also this calculation
can be done just for the isotropic (and, therefore, the simplest)
case. For examples, see TABLE 1. These parameter values do not
change. Only the crack density parameter, the crack orientation
distributions, and possibly the crack shapes, etc., change.
For very dilute fracture systems, any of the standard effective medium
theories will actually produce virtually the same values of the
parameters
ant, 1997; Grechka, 2005);
and also this calculation
can be done just for the isotropic (and, therefore, the simplest)
case. For examples, see TABLE 1. These parameter values do not
change. Only the crack density parameter, the crack orientation
distributions, and possibly the crack shapes, etc., change.
For very dilute fracture systems, any of the standard effective medium
theories will actually produce virtually the same values of the
parameters 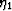 and
and 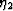 .The only variable is the crack shape, which I have assumed here
(as is most commonly done) to be penny-shaped cracks with small
aspect ratios. Values of
.The only variable is the crack shape, which I have assumed here
(as is most commonly done) to be penny-shaped cracks with small
aspect ratios. Values of 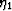 and
and 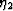 can vary with changes
in the assumed microstructure (i.e., other choices of crack shapes), but
values could be tabulated once and for all for the low density limit
with any choices of crack shape we might ever want to consider and then
the numbers would be universally available. Users would not need to
be experts in effective medium theory to make use of these results --
although they would, of course, still need to be experts in the
interpretation of seismic data and, in particular, of the Thomsen
parameters themselves.
can vary with changes
in the assumed microstructure (i.e., other choices of crack shapes), but
values could be tabulated once and for all for the low density limit
with any choices of crack shape we might ever want to consider and then
the numbers would be universally available. Users would not need to
be experts in effective medium theory to make use of these results --
although they would, of course, still need to be experts in the
interpretation of seismic data and, in particular, of the Thomsen
parameters themselves.
REFERENCES
-
Al-Husseini, M. I., Glover, J. B., and Barley, B. J., 1981,
Dispersion patterns of the ground-roll in eastern Saudi Arabia:
Geophysics 46 (2), 121-137.
-
Berge, P. A., Berryman, J. G., and Bonner, B. P., 1993a, Influence of
microstructure on rock elastic properties: Geophys. Res. Lett.,
20, 2619-2622.
-
Berge, P. A., Bonner, B. P., and Berryman, J. G., 1995, Ultrasonic
velocity-porosity relationships for sandstone analogs made from fused
glass beads: Geophysics, 60, 108-119.
-
Berryman, J. G., 1980, Long-wavelength propagation in composite elastic
media II. Ellipsoidal inclusions: J. Acoust. Soc. Am.,
68, 1820-1831.
-
Berryman, J. G., 1995, Mixture theories for rock properties: in American
Geophysical Union Handbook of Physical Constants, edited by
T. J. Ahrens, AGU, New York, pp. 205-228.
-
Berryman, J. G., 1999, Origin of Gassmann's equations:
Geophysics, 64, 1627-1629. [tutorial]
-
Berryman, J. G., 2004, Modeling high-frequency acoustic velocities in
patchy and partially saturated porous rock using differential
effective medium theory: Int. J. Multiscale Computational
Engineering, 2 (1), 115-131.
-
Berryman, J. G., and Pride, S. R., 2002a,
Models for computing geomechanical constants of double-porosity
materials from the constituents properties:
J. Geophys. Res., 107(B3), 10.1029/2000JB000108, March
28 (2002).
-
Berryman, J. G., Pride, S. R., and Wang, H. F., 2002b,
A differential scheme for elastic properties of rocks with dry or
saturated cracks: Geophys. J. Int., 151 (2), 597-611.
-
Berryman, J. G., Thigpen, L., and Chin, R. C. Y., 1988, Bulk elastic wave
propagation in partially saturated porous solids:
J. Acoust. Soc. Am., 84, 360-373.
-
Berryman, J. G., and Wang, H. F., 2000, Elastic wave propagation and
attenuation in a double-porosity dual-permeability medium:
in Proceedings of the Neville G. W. Cook Conference,
LBNL, October 16-17, 1998, Int. J. Rock Mech.,
37, 2000.
-
Biot, M. A., 1956a, Theory of propagation of elastic waves in a
fluid-saturated porous solid. I. Low-frequency range:
J. Acoust. Soc. Am., 28, 168-178.
-
Biot, M. A., 1956b, Theory of propagation of elastic waves in a
fluid-saturated porous solid. II. Higher frequency range:
J. Acoust. Soc. Am., 28, 179-191.
-
Biot, M. A., 1962, Mechanics of deformation and acoustic propagation in porous
media: J. Appl. Phys., 33, 1482-1498.
-
Biot, M. A., and Willis, D. G., 1957, The elastic coefficients of the
theory of consolidation: J. App. Mech., 24, 594-601.
-
Budiansky, B., and O'Connell, R. J., 1976, Elastic moduli of a cracked solid:
Int. J. Solids Struc., 12, 81-97.
-
Dvorkin, J. and Nur, A., 1998, Acoustic signatures of patchy saturation:
Int. J. Solids Struct., 35, 4803-4810.
-
Endres, A. L., and Knight, R., 1989, The effect of microscopic fluid
distribution on elastic wave velocities: Log Anal.
30, 437-444.
-
Ewing, W. M., Jardetsky, W. S., and Press, F., 1957, Elastic Waves in
Layered Media, McGraw-Hill, New York.
-
Gassmann, F., 1951, Über die elastizität poröser medien:
Veirteljahrsschrift der Naturforschenden Gesellschaft in Zürich,
96, 1-23.
-
Grechka, V., 2005, Penny-shaped fractures revisited:
Stud. Geophys. Geod., 49, 365-381.
-
Grechka, V., and Kachanov, M., 2006, Effective elasticity of fractured
rocks: The Leading Edge, 25, 152-155.
-
Henyey, F. S., and Pomphrey, N., 1982, Self-consistent elastic moduli
of a cracked solid: Geophys. Res. Lett., 9 (8), 903-906.
-
Hildebrand, F. B., 1956, Introduction to Numerical Analysis,
Dover Publications, New York, pp. 575-578pa.
-
Hornby, B. E., 1994, The Elastic Properties of Shales,
Ph.D. dissertation, University of Cambridge, Cambridge, UK.
-
Hudson, J. A., 1980, Wave speeds and attenuation of elastic waves in
material containing cracks: Geophys. J. R. Astron. Soc., 64,
133-150.
-
Hudson, J. A., 1994, Overall properties of a material with inclusions or
cavities: Geophys. J. Int., 117, 555-561.
-
Ji, C., Tsuboi, S., Komatitsch, D., and Tromp, J., 2005,
Rayleigh-wave multipathing along the west coast of North America:
Bull. Seismol. Soc. Am., 95 (6), 2115-2124.
-
Johnson, D. L., 2001, Theory of frequency dependent acoustics in
patchy-saturated porous media: J. Acoust. Soc. Am., 110,
682-694.
-
Kachanov, M., 1994, Elastic solids with many cracks and related
problems: in Advances in Applied Mechanics, edited by
J. W. Hutchinson and T. Y. Wu,
Academic Press, Boston, Massachusetts, pp. 260-445.
-
Lynn, H. B., Simon, K. M., Layman, M., Schneider, R., Bates, C. R.,
and Jones, M., 1995, Use of anisotropy in P-wave and S-wave data
for fracture characterization in a naturally fractured gas reservoir:
The Leading EDge 14, 887-893.
-
Mavko, G., and Jizba, D., 1991, Estimating grain-scale fluid effects
on velocity dispersion in rocks: Geophysics, 56, 1940-1949.
-
Mavko, G., and Nolen-Hoeksema, R., 1994, Estimating seismic velocities at
ultrasonic frequencies in partially saturated rocks: Geophysics,
59, 252-258.
-
Murphy, William F., III, 1982, Effects of Microstructure and Pore
Fluids on the Acoustic Properties of Granular Sedimentary Materials,
Ph.D. Dissertation, Stanford University, Stanford, CA.
-
Murphy, William F., III, 1984, Acoustic measures of partial gas saturation
in tight sandstones: J. Geophys. Res., 89, 11549-11559.
-
Musgrave, M. J. P., 1959, The propagation of elastic waves in crystals and
other anisotropic media: Reports Prog. Phys., 22, 74-96.
-
O'Connell, R. J., and Budiansky, B., 1977, Viscoelastic properties of
fluid-saturated cracked solids: J. Geophys. Res., 82,
5719-5736.
-
Prat, P. C., and Ba
 ant, Z. P., 1997, Tangential stiffness
of elastic materials with systems of growing or closing cracks:
J. Mech. Phys. Solids, 45, 611-636.
ant, Z. P., 1997, Tangential stiffness
of elastic materials with systems of growing or closing cracks:
J. Mech. Phys. Solids, 45, 611-636.
-
Press, W. H., Flannery, B. P., Teukolsky, S. A., and Vetterling, W. T.,
1988, Numerical Recipes in C: The Art of Scientific Computing,
Cambridge University Press, New York, pp. 270-275.
-
Pride, S. R., 2005, Relationships between seismic and hydrological
properties: in Hydrogeophysics, edited by Y. Rubin and
S. Hubbard, Springer, New York, pp. 253-291.
-
Pride, S. R., and Berryman, J. G., 2003,
Linear dynamics of double-porosity dual-permeability materials
I. Governing equations and acoustic attenuation:
Physical Review E, 68, 036603 (September 9, 2003).
-
Pride, S. R., and J. G. Berryman, J. G., 2003,
Linear dynamics of double-porosity dual-permeability materials
II. Fluid transport equations:
Physical Review E, 68, 036604 (September 9, 2003).
-
Pride, S. R., Berryman, J. G., and Harris, J. M., 2004,
Seismic attenuation due to wave-induced flow: J. Geophys. Res.,
109, B01201 (January 14, 2004).
-
Pride, S. R., Harris, J. M., et al., 2003,
Permeability dependence of seismic amplitudes:
The Leading Edge,22, 518-525.
-
Rathore, J. S., Fjaer, E., Holt, R. M., and Renlie, L., 1995,
Acosutic anisotropy of a synthetic sanstone with controlled crack geometry:
Geophys. Prosp., 43, 711-728.
-
Rüger, A., 1998, Variation of P-wave reflectivity with offset and azimuth
in anisotropic media: Geophysics, 63, 935-947.
-
Rüger, A., 2002, Reflection Coefficients and Azimuthal AVO Analysis in
Anisotropic Media, Geophysical Monographs Series, Number 10, SEG,
Tulsa, OK.
-
Sayers, C. M., and Kachanov, M., 1991, A simple technique for finding
effective elastic constants of cracked solids for arbitrary crack
orientation statistics: Int. J. Solids Struct.,
27, 671-680.
-
Sayers, C. M., and Kachanov, M., 1995, Microcrack-induced elastic wave
anisotropy of brittle rocks: J. Geophys. Res, 100,
4149-4156.
-
Thomsen, L., 1986, Weak elastic anisotropy: Geophysics, 51,
1954-1966.
-
Thomsen, L., 1995, Elastic anisotropy due to aligned cracks in porous media:
Geophys. Prosp., 43, 805-829.
-
Thomsen, L., 2002, Understanding Seismic Anisotropy in Exploration and
Exploitation, 2002 Distinguished Instructuor Short Course, Number 5,
SEG, Tulsa, OK.
-
Tod, S. R., 2002, The effects of stress and fluid pressure on the
anisotropy of interconnected cracks: Geophys. J. Int.,
149, 149-156.
-
Tod, S. R., 2003, An anisotropic fractured poroelastic effective medium
theory: Geophys. J. Int., 155, 1006-1020.
-
Wawersik, W. R., Orr, F. M., Rudnicki, J. W., Ortoleva, P. J., Dove, P.,
Richter, F., Harris, J., Warpinski, N. R., Logan, J. M., Wilson, J. L.,
Pyrak-Nolte, L., and Wong, T.-F., 2001, Terrestrial sequestration of
CO2: An assessment of research needs: Advances in Geophysics,
43, 97-177.
-
Weertman, J., 1996, Dislocation-Based Fracture Mechanics,
World Scientific, River Edge, NJ.
-
Zimmerman, R. W., 1991, Compressibility of Sandstones, Elsevier, Amsterdam.





Next: About this document ...
Up: Berryman: Seismic waves in
Previous: Shallow example
Stanford Exploration Project
4/5/2006
![]() and
and ![]() can be
determined in a straightforward way using any effective medium theory
we trust (Kachanov, 1994; Prat and Ba
can be
determined in a straightforward way using any effective medium theory
we trust (Kachanov, 1994; Prat and Ba![]() ant, 1997; Grechka, 2005);
and also this calculation
can be done just for the isotropic (and, therefore, the simplest)
case. For examples, see TABLE 1. These parameter values do not
change. Only the crack density parameter, the crack orientation
distributions, and possibly the crack shapes, etc., change.
For very dilute fracture systems, any of the standard effective medium
theories will actually produce virtually the same values of the
parameters
ant, 1997; Grechka, 2005);
and also this calculation
can be done just for the isotropic (and, therefore, the simplest)
case. For examples, see TABLE 1. These parameter values do not
change. Only the crack density parameter, the crack orientation
distributions, and possibly the crack shapes, etc., change.
For very dilute fracture systems, any of the standard effective medium
theories will actually produce virtually the same values of the
parameters ![]() and
and ![]() .The only variable is the crack shape, which I have assumed here
(as is most commonly done) to be penny-shaped cracks with small
aspect ratios. Values of
.The only variable is the crack shape, which I have assumed here
(as is most commonly done) to be penny-shaped cracks with small
aspect ratios. Values of ![]() and
and ![]() can vary with changes
in the assumed microstructure (i.e., other choices of crack shapes), but
values could be tabulated once and for all for the low density limit
with any choices of crack shape we might ever want to consider and then
the numbers would be universally available. Users would not need to
be experts in effective medium theory to make use of these results --
although they would, of course, still need to be experts in the
interpretation of seismic data and, in particular, of the Thomsen
parameters themselves.
can vary with changes
in the assumed microstructure (i.e., other choices of crack shapes), but
values could be tabulated once and for all for the low density limit
with any choices of crack shape we might ever want to consider and then
the numbers would be universally available. Users would not need to
be experts in effective medium theory to make use of these results --
although they would, of course, still need to be experts in the
interpretation of seismic data and, in particular, of the Thomsen
parameters themselves.