Computational cost savings

For a data cube with dimensions $n=n_1 \times n_2 \times n_3$, each iteration requires n₁ forward and reverse 2D FFTs. Therefore, in 2D the number of operations per iteration is about $8 n (1+\log(4 n_2 n_3))$ for the FFT method. For the DCT method, the number of operations per iteration is about $8 n+2n\log( n_2 n_3)$. In 3D the FFT method requires about $8 n (1+\log(8 n))$ operations where as the DCT only requires $8 n+2n\log(n)$. Because there is a certain about of overhead in each iteration common to both algorithms, the actually cost saving is typically a factor of two to four in 2D and three to five in 3D depending on the size of the problem.

The DCT method also has a significant advantage in memory usage as compared to the DCT. Without requiring mirroring, the DCT saves a factor of four in 2D and eight in 3D, however, again there is a certain amount of overhead common to both algorithms. In 2D, the DCT requires about 9n memory allocation as opposed to the 23n memory of the FFT algorithm. In 3D, the DCT requires still about 9n where as the FFT jumps up to 39n. In summary, the DCT saves greater than a factor of two in 2D and greater than a factor of four in 3D in memory requirements.

 

plane3D Figure 1 The dipping planes synthetic model. Although a trivial flattening test case, the boundaries of the divergence of the dip are not periodic.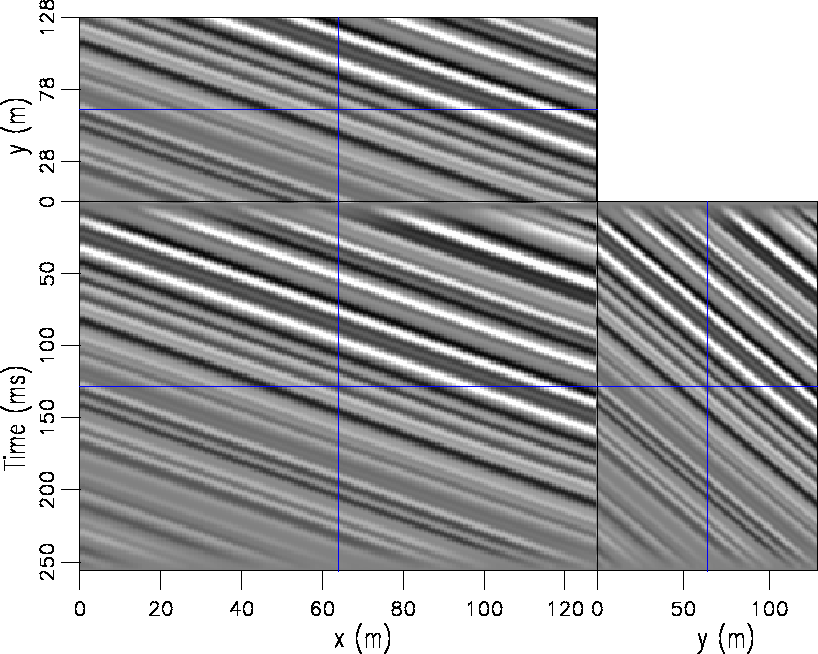

 

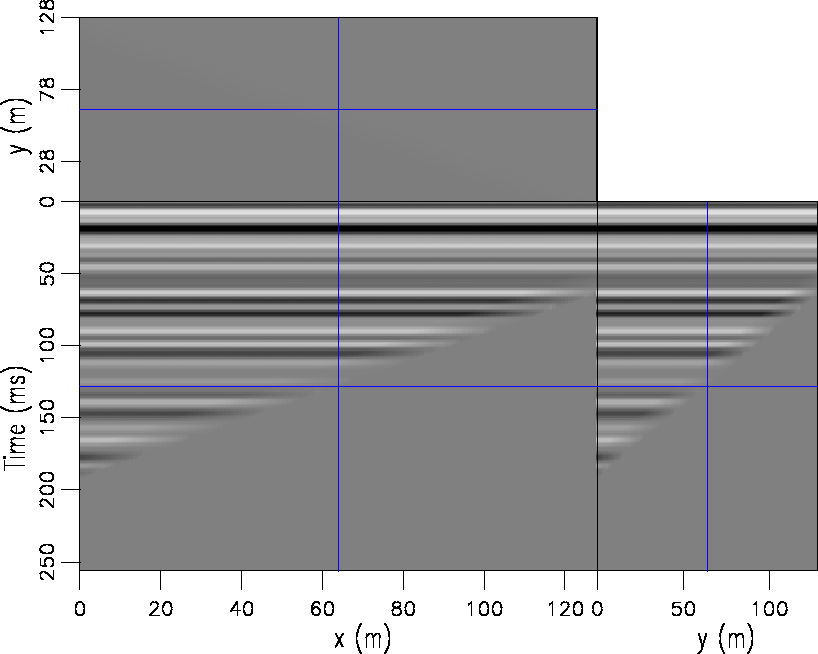
plane3D.fft_mirr.flat_cos Figure 2 The data in Figure flattened using the FFT method with mirrors.