Methodology

Normalized cuts image segmentation partitions images into two groups. To do this, it first creates weights relating each sample to randomly selected samples along paths within local neighborhoods. These weights are stored in a sparse matrix 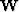${\bf W}$. It then finds the cut that partitions the image into two groups, A and B, by minimizing the normalized cut:  

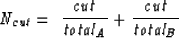$${\it N_{\it cut} =\ {{\it cut}\over {\it total_A} } + {{\it cut}\over {\it total_B}} }$$ (1)

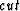where ${\it cut}$ is the sum of the weights cut by the partition. 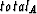${\it total_A}$ is the sum of all weights in Group A, and 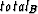${\it total_B}$ is the sum of all weights in Group B. Normalizing the cut by the sum of all the weights in each group prevents the partition from selecting overly-small groups of nodes.

The minimum of 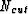${\it N_{cut}}$ can be found by solving the generalized eigensystem:  

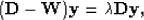$$({\bf D} - {\bf W})\bf y =\lambda {\bf D}\bf y,$$ (2)

created from the weight matrix (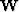${\bf W}$) and a diagonal matrix (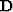${\bf D}$), with each value on the diagonal being the sum of each column of 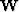${\bf W}$. The eigenvector (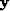${\bf y}$) with the second smallest eigenvalue (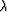${\lambda}$) is used to partition the image by taking all values greater than zero to be in one group, and its complement to be in the other. For a more detailed description, see Shi and Malik (2000).

 

• Application to seismic
• Random bounds
• 3D implementation