Next: Concluding Remarks
Up: Numerical Examples
Previous: Wave-equation generated Green's Functions
Seismic data acquired on topography usually require significant
preprocessing before any imaging technique can be applied
successfully. Performing wave-equation migration, though, usually
requires that data exist on regularly sampled meshes before a
wavefield extrapolation procedure can begin. Usually, this involves a
data regularization step implemented as either pre-migration
datuming or through a wavefield injection plus interpolation migration
strategy.
An alternative to these standard approaches is discussed in
Shragge and Sava (2005), who pose seismic imaging directly in
acquisition coordinates and use Riemannian wavefield extrapolation to
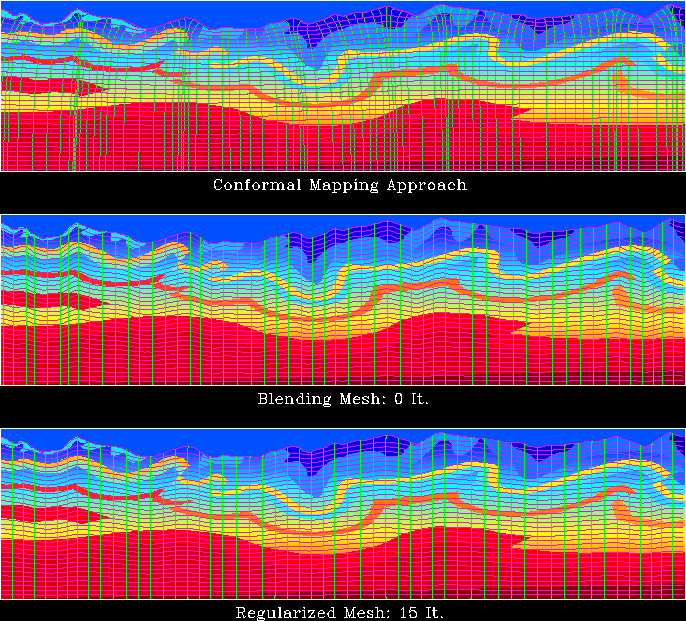
propagate wavefields. Initially, a conformal mapping approach was
used to generate structured, locally orthogonal coordinate meshes (see
top panel of figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). However, the ensuing grid
clustering and rarefaction demanded by orthogonality led to
significant spatial variance in metric tensor
coefficients. Importantly, this variance caused artifacts in the
resulting image, which remains the main drawback of this migration
approach.
). However, the ensuing grid
clustering and rarefaction demanded by orthogonality led to
significant spatial variance in metric tensor
coefficients. Importantly, this variance caused artifacts in the
resulting image, which remains the main drawback of this migration
approach.
Topography
Figure 3 Meshing example for the
wave-equation migration from topography application. Top panel:
Locally orthogonal coordinate system calculated by conformal mapping
Shragge and Sava (2005). Note the severe amount of grid
clustering indicating a need for meshing regularization. Middle
panel: Blended coordinate system 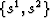 forming the
differential gridding algorithm input. Bottom panel: Regularized
mesh
forming the
differential gridding algorithm input. Bottom panel: Regularized
mesh 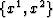 after 15 iterations.
after 15 iterations.





The extension of RWE to non-orthogonal coordinate systems
Shragge (2006) allows for greater flexibility in
coordinate system design. The middle panel in
figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) represents a blended coordinate system
represents a blended coordinate system  that forms the input to the differential mesh algorithm.
Lines predominantly in the horizontal direction mimic topography in
the near-surface and slowly heal to form an evenly sampled wavefield
at depth. The bottom panel shows the coordinate system output
that forms the input to the differential mesh algorithm.
Lines predominantly in the horizontal direction mimic topography in
the near-surface and slowly heal to form an evenly sampled wavefield
at depth. The bottom panel shows the coordinate system output 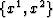 from the gridding algorithm after 15 iterations. Grid
irregularities now heal more rapidly and the mesh becomes very regular
after a few extrapolation steps into the subsurface.
from the gridding algorithm after 15 iterations. Grid
irregularities now heal more rapidly and the mesh becomes very regular
after a few extrapolation steps into the subsurface.





Next: Concluding Remarks
Up: Numerical Examples
Previous: Wave-equation generated Green's Functions
Stanford Exploration Project
4/5/2006
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). However, the ensuing grid
clustering and rarefaction demanded by orthogonality led to
significant spatial variance in metric tensor
coefficients. Importantly, this variance caused artifacts in the
resulting image, which remains the main drawback of this migration
approach.
). However, the ensuing grid
clustering and rarefaction demanded by orthogonality led to
significant spatial variance in metric tensor
coefficients. Importantly, this variance caused artifacts in the
resulting image, which remains the main drawback of this migration
approach.