




Next: Numerical Examples
Up: Shragge: Differential gridding methods
Previous: Regularization through Monitor Functions
Generating a 2-D coordinate system through differential methods requires
solving for coordinates 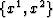 within domain X2.
Incorporating l monitor functions for grid regularization expands
the dimensionality of the mapping to,
within domain X2.
Incorporating l monitor functions for grid regularization expands
the dimensionality of the mapping to,
| 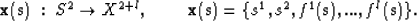 |
(9) |
Coordinate system 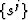 is related to an underlying Cartesian
grid, which is chosen to be a unit square defined by
is related to an underlying Cartesian
grid, which is chosen to be a unit square defined by 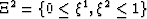 . Transformation
. Transformation 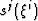 is assumed to be
piece-wise smooth and known on the boundary of
is assumed to be
piece-wise smooth and known on the boundary of 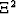 such that:
such that: 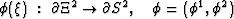 .
Within this framework, the 2-D gridding equations become,
.
Within this framework, the 2-D gridding equations become,
| ![\begin{eqnarray}
D^{\xi}[s^j] = - D^{\xi} [ f^k ] \frac{\partial f^k}{\partial s...
...l \Xi^2} =
\mathbf{\phi}(\mathbf{\xi}), \quad j=1,2, \quad k=1,l,\end{eqnarray}](img36.gif) |
(10) |
where Laplacian operator ![$D^{\xi}[\cdot]$](img37.gif) and metric tensor gij
are written explicitly Liseikin (2004),
and metric tensor gij
are written explicitly Liseikin (2004),
| ![\begin{eqnarray}
D^{\xi}[v] = & g_{22}^{\xi} \frac{\partial^2 v}{\partial \xi^1
...
...}(\mathbf{\xi})] }{\partial \xi^j},
\quad i,j,k=1,2, \quad m=1,l.\end{eqnarray}](img38.gif) |
(11) |
| (12) |
One convenient way to solve the set of elliptical
equations 10 is by transforming them to a set of
parabolic equations (i.e. include time-dependence) that have a common
steady-state solution. Thus, equations 10 are
reformulated to include time-dependence - 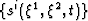 -
leading to the six governing equations,
-
leading to the six governing equations,
| ![\begin{eqnarray}
\frac{ \partial s^1}{ \partial t} = D[s^1] + D[ f^k] \frac{\par...
...1,\xi^2), & t=0 \
s^2(\xi^1,\xi^2,0) = s^2_0(\xi^1,\xi^2), & t=0\end{eqnarray}](img40.gif) |
(13) |
| (14) |
| (15) |
| (16) |
| (17) |
| (18) |
Solutions 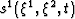 and
and 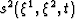 satisfying
equations 13-18 will converge to the
solutions
satisfying
equations 13-18 will converge to the
solutions 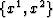 of equations 10 as
of equations 10 as 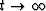 . Hence, the answer to within tolerance factor
. Hence, the answer to within tolerance factor
 occurs at some Tn. Details of an iterative scheme and an
algorithm for computation to solve equations 13 are
provided in Appendix A.
occurs at some Tn. Details of an iterative scheme and an
algorithm for computation to solve equations 13 are
provided in Appendix A.





Next: Numerical Examples
Up: Shragge: Differential gridding methods
Previous: Regularization through Monitor Functions
Stanford Exploration Project
4/5/2006
![\begin{eqnarray}
D^{\xi}[v] = & g_{22}^{\xi} \frac{\partial^2 v}{\partial \xi^1
...
...}(\mathbf{\xi})] }{\partial \xi^j},
\quad i,j,k=1,2, \quad m=1,l.\end{eqnarray}](img38.gif)
![]() -
leading to the six governing equations,
-
leading to the six governing equations,
![\begin{eqnarray}
\frac{ \partial s^1}{ \partial t} = D[s^1] + D[ f^k] \frac{\par...
...1,\xi^2), & t=0 \
s^2(\xi^1,\xi^2,0) = s^2_0(\xi^1,\xi^2), & t=0\end{eqnarray}](img40.gif)