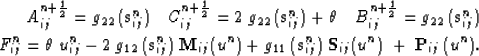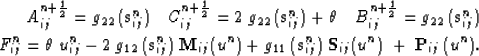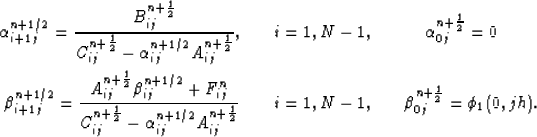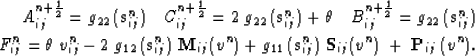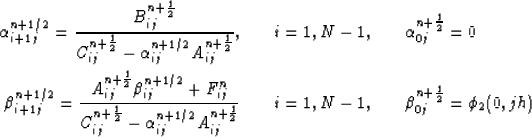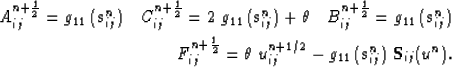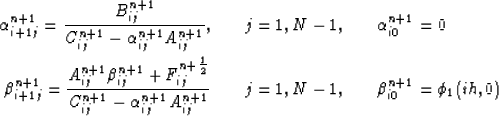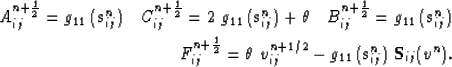Next: Step-by-Step Algorithm
Up: REFERENCES
Previous: REFERENCES
The solution to the finite difference scheme is obtained through
recursive back-substitution.
Equation 31 - is solved by,
| 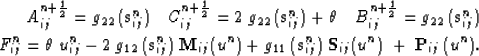 |
|
| (43) |
The solution for a fixed number j in range 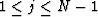 obtained through,
obtained through,
| 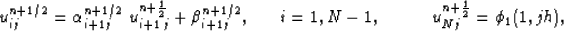 |
(44) |
where,
Equation 32 - is solved by,
| 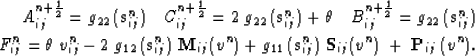 |
|
| (45) |
The solution for a fixed j in range 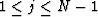 is obtained
through,
is obtained
through,
| 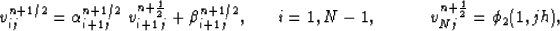 |
(46) |
where,
Equation 33 - is solved by,
| 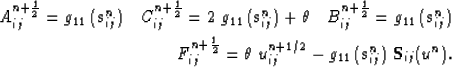 |
|
| (47) |
The solution for a fixed i in the range 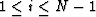 is
obtained
through,
is
obtained
through,
| 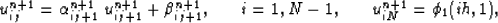 |
(48) |
where,
Equation 34 - is solved by,
| 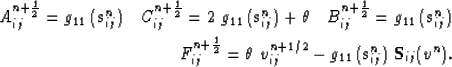 |
|
| (49) |
The solution for a fixed i in the range 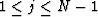 is
obtained through,
is
obtained through,
| 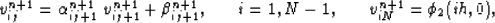 |
(50) |
where,
An approximate solution of the equations 19 will be
found at some large time TN that satisfies,
| 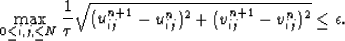 |
(51) |





Next: Step-by-Step Algorithm
Up: REFERENCES
Previous: REFERENCES
Stanford Exploration Project
4/5/2006