




Next: Phase correction filter
Up: Shan: Implicit migration for
Previous: Optimized one-way wave equation
For the second-order approximation (m=1,n=1), equation (9) is the following
cascaded partial differential equation in the space domain:
|  |
(11) |
| (12) |
In isotropic migration, 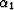 and
and 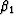 are constant. In VTI media,
are constant. In VTI media, 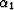 and
and 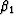 are
functions of the anisotropy parameters
are
functions of the anisotropy parameters  and
and 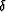 . For laterally varying media, the value of
. For laterally varying media, the value of 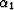 and
and
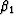 also vary laterally. It is too expensive to calculate
also vary laterally. It is too expensive to calculate 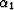 and
and 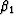 for each grid point during the
wavefield extrapolation. I calculate
for each grid point during the
wavefield extrapolation. I calculate 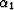 and
and 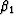 for a range of
for a range of  and
and 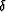 and store them
in a table before the migration. I then generate maps of
and store them
in a table before the migration. I then generate maps of 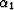 and
and 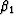 from the table.
With the map of the coefficents
from the table.
With the map of the coefficents 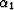 and
and 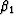 , the finite-difference scheme for VTI media can be performed in the same way as an isotropic migration.
, the finite-difference scheme for VTI media can be performed in the same way as an isotropic migration.





Next: Phase correction filter
Up: Shan: Implicit migration for
Previous: Optimized one-way wave equation
Stanford Exploration Project
4/5/2006

