Next: Discussion
Up: Methodology for attenuating the
Previous: Adjoint migration
This step is subdivided into two tasks: adaptive matching of the multiples
to the original data and subtraction of the matched multiples to get
the primaries Guitton (2005). To
assess the ability of adaptive subtraction to restore the amplitudes lost
by the migration-adjoint migration process, I applied
it to the adjoint-migrated, unmuted SODCIGs (panel (b) of
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). Figure
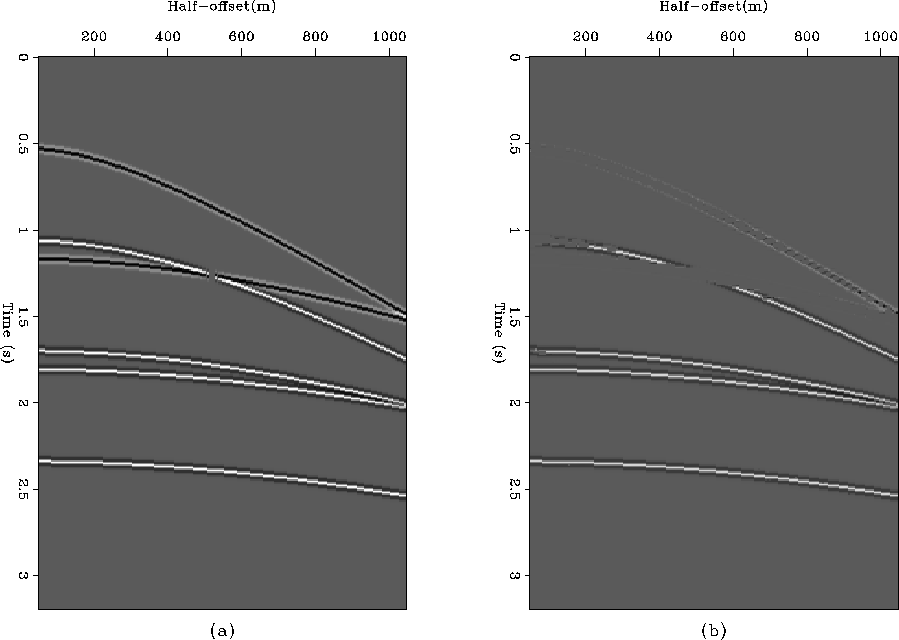
). Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the original [panel (a)] and the matched [panel (b)] CMP.
Figure
shows the original [panel (a)] and the matched [panel (b)] CMP.
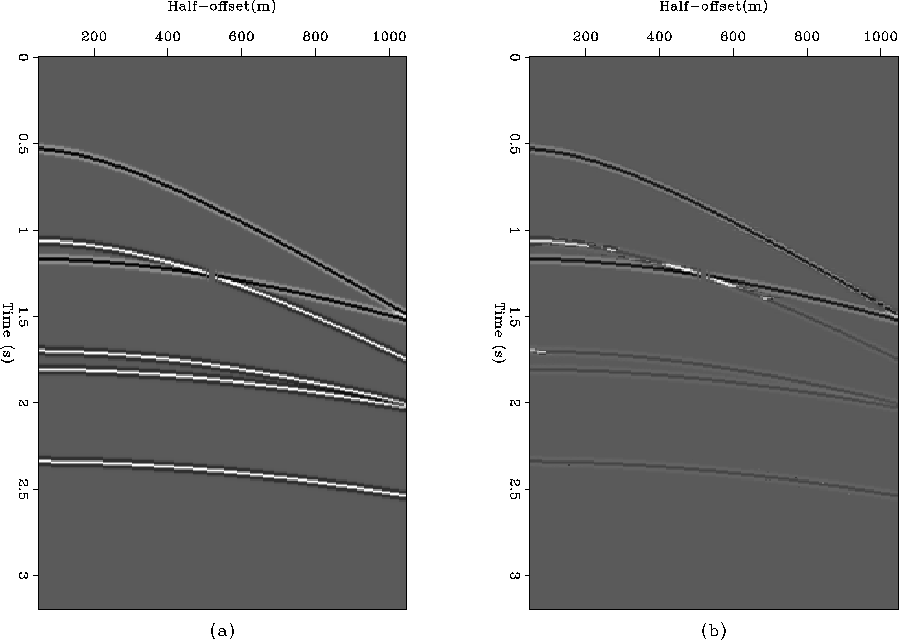
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the difference between the two panels in
Figure
shows the difference between the two panels in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) plotted with 100% clip and with the
clip of the original data. The adaptive pattern matching has recovered the
the original data remarkably well despite the loss of energy on the
large offsets of the water-bottom primary and multiple after the
migration-adjoint migration process (see panel (b) of
Figure
plotted with 100% clip and with the
clip of the original data. The adaptive pattern matching has recovered the
the original data remarkably well despite the loss of energy on the
large offsets of the water-bottom primary and multiple after the
migration-adjoint migration process (see panel (b) of
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
cmp_comp2
).
cmp_comp2
Figure 7 Comparison between a CMP of the original data
(a) and the same CMP after migration, adjoint migration and adaptive matching
(b).




 resid1
resid1
Figure 8 Residual energy after subtracting the
matched CMP from the original, plotted at 100% clip (a) and at
the clip of the original CMP (b).





We would like to similarly match the estimated multiples to the original
data but we cannot, because nothing prevents the pattern-matching
algorithm from attempting to match the primaries as well. This is obviously
undesirable because, as much as possible, we want to keep the primaries as
they are in the original data. Here is where the estimate of the primaries
will help. We can estimate filters to simultaneously match both the estimated
primaries and the estimated multiples to the data as in Guitton's thesis
2005 thus preventing the primaries to be matched
to the same dataset as the multiples. An easier approach is to use
the estimated primaries to compute a mask such that
where the primaries are present the mask is zero and therefore the primaries
are not matched when attempting to match the multiples Claerbout and Fomel (2002) . This is
the approach I used here although in practice the other approach is likely
to be better. In order to compute the mask I first computed the envelope
of the estimated
primaries, and then chose a threshold amplitude above which all samples
were set to zero and below which all samples were set to one. This mask was
then smoothed with a triangular filter both in offset and in time.
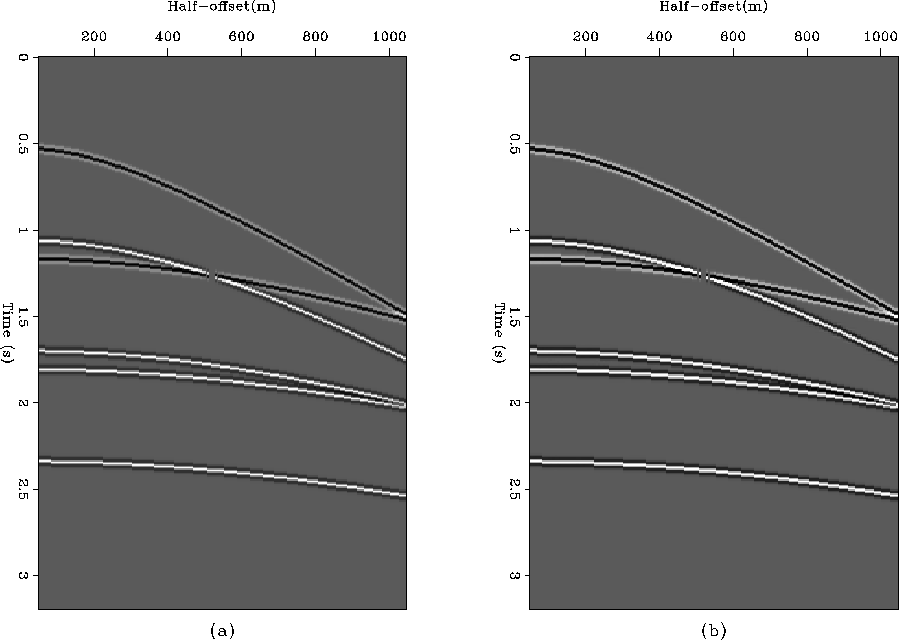
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the envelope of the estimated primaries and
the mask.
shows the envelope of the estimated primaries and
the mask.
mask
Figure 9 Envelope of the estimated primaries (a)
and mask of ones and zeros derived from it (b).





The result of applying the weighted adaptive matching to the estimated
multiples is shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The water-bottom multiple
has not been well recovered, in contrast to the other multiples. The
primaries didn't leak much into the multiples, which is a very satisfactory
result. Figure
. The water-bottom multiple
has not been well recovered, in contrast to the other multiples. The
primaries didn't leak much into the multiples, which is a very satisfactory
result. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the residual, obtained by subtracting
the matched estimated multiples from the data. Here we see that although the
result is not perfect, most of the multiple energy has been attenuated
except for the water-bottom multiple. In particular, the primaries have
been well-recovered.
shows the residual, obtained by subtracting
the matched estimated multiples from the data. Here we see that although the
result is not perfect, most of the multiple energy has been attenuated
except for the water-bottom multiple. In particular, the primaries have
been well-recovered.
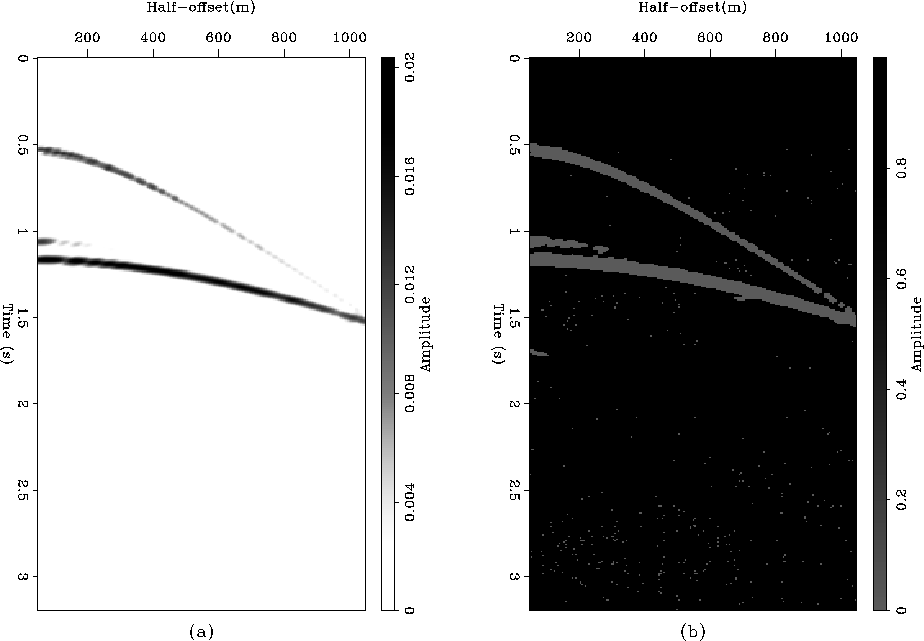
cmp_comp3
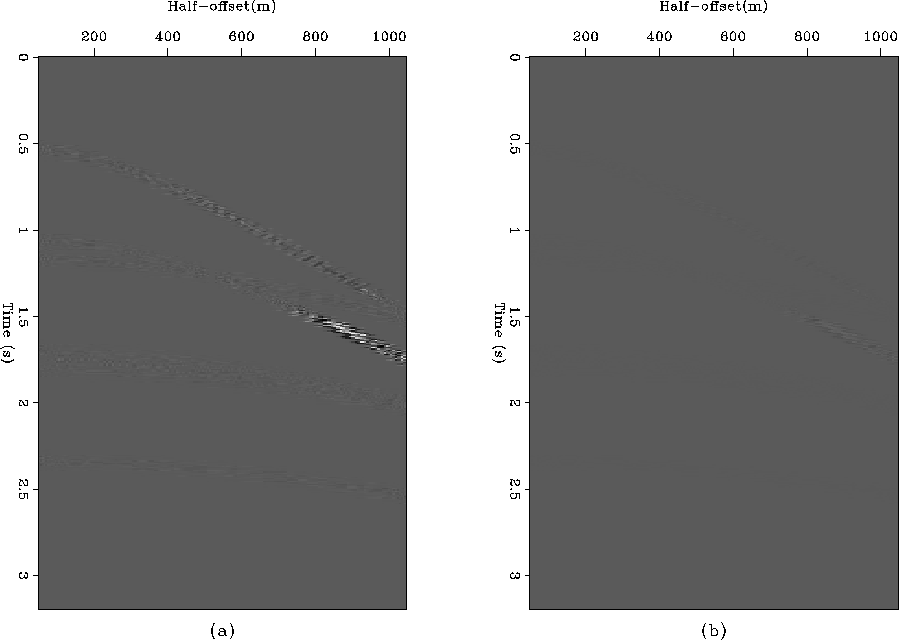
Figure 10 Comparison between a CMP of the original data
(a) and the same CMP after migration, muting of the primaries,
adjoint migration and adaptive matching (b). Some residual energy
from the large offset of the water-bottom primary remains and the
water-bottom multiple has been imperfectly recovered.




 resid2
resid2
Figure 11 Residual energy after subtracting the
matched CMP of the multiples from the original, plotted at 100% clip
(a) and at the clip of the original CMP (b).










Next: Discussion
Up: Methodology for attenuating the
Previous: Adjoint migration
Stanford Exploration Project
4/5/2006
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). Figure
). Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the original [panel (a)] and the matched [panel (b)] CMP.
Figure
shows the original [panel (a)] and the matched [panel (b)] CMP.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the difference between the two panels in
Figure
shows the difference between the two panels in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) plotted with 100% clip and with the
clip of the original data. The adaptive pattern matching has recovered the
the original data remarkably well despite the loss of energy on the
large offsets of the water-bottom primary and multiple after the
migration-adjoint migration process (see panel (b) of
Figure
plotted with 100% clip and with the
clip of the original data. The adaptive pattern matching has recovered the
the original data remarkably well despite the loss of energy on the
large offsets of the water-bottom primary and multiple after the
migration-adjoint migration process (see panel (b) of
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
).

![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the envelope of the estimated primaries and
the mask.
shows the envelope of the estimated primaries and
the mask.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The water-bottom multiple
has not been well recovered, in contrast to the other multiples. The
primaries didn't leak much into the multiples, which is a very satisfactory
result. Figure
. The water-bottom multiple
has not been well recovered, in contrast to the other multiples. The
primaries didn't leak much into the multiples, which is a very satisfactory
result. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the residual, obtained by subtracting
the matched estimated multiples from the data. Here we see that although the
result is not perfect, most of the multiple energy has been attenuated
except for the water-bottom multiple. In particular, the primaries have
been well-recovered.
shows the residual, obtained by subtracting
the matched estimated multiples from the data. Here we see that although the
result is not perfect, most of the multiple energy has been attenuated
except for the water-bottom multiple. In particular, the primaries have
been well-recovered.