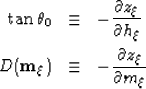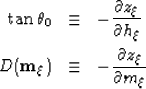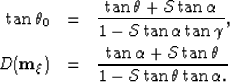Next: REFERENCES
Up: Rosales et al.: PS-ADCIG
Previous: Acknowledgments
This appendix presents the derivation of the main
equation for this paper, that is, the transformation
from the subsurface offset domain into the angle domain
for converted-wave data.
Rosales and Biondi (2005) present the
derivation for the angle-domain transformation.
Biondi (2005) and Shragge et al. (2005)
present similar equations for different applications,
for anisotropic case and for the forward-scatter case,
respectively.
Throughout this Appendix we will use the following
defintions:
In this definitions, 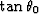 is the pseudo-reflection angle,
and
is the pseudo-reflection angle,
and 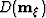 is field for the local image dips. The bases for this
definition resides in the conventional PP case. For that
case, the pseudo-reflection angle represents the
reflection angle, and the field
is field for the local image dips. The bases for this
definition resides in the conventional PP case. For that
case, the pseudo-reflection angle represents the
reflection angle, and the field 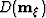 represents the
geological dip Fomel (1996).
Based on this definition,
the angle equations from
Biondi (2005); Rosales and Biondi (2005); Shragge et al. (2005)
can be rewritten as:
represents the
geological dip Fomel (1996).
Based on this definition,
the angle equations from
Biondi (2005); Rosales and Biondi (2005); Shragge et al. (2005)
can be rewritten as:
| 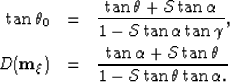 |
(6) |
| (7) |
Following basic algebra, equation 7 can be rewritten as:
| 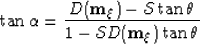 |
(8) |
Substituing equation 8 into equation 6,
and following basic algebraic manipulations, we obtain equation 4
in the paper.





Next: REFERENCES
Up: Rosales et al.: PS-ADCIG
Previous: Acknowledgments
Stanford Exploration Project
4/5/2006