




Next: Extension to N-D
Up: R. Clapp: A modified
Previous: R. Clapp: A modified
Lloyd's 1-D method
attempts to identify the major features in a signal's
histogram as
accurately as possible,
with as few points as possible.
The selected points are referred to as the signal's
``codebook''.
The methodology is iterative in nature. It starts
from an initial code book, then repeats
- 1
- Find for every point the closest codebook entry. These points form a cell.
- 2
- Find the average of all points associated with a given codebook
entry. The average becomes the new codebook entry.
- 3
- Remove codebook entries that have no, or few, points associated with them.
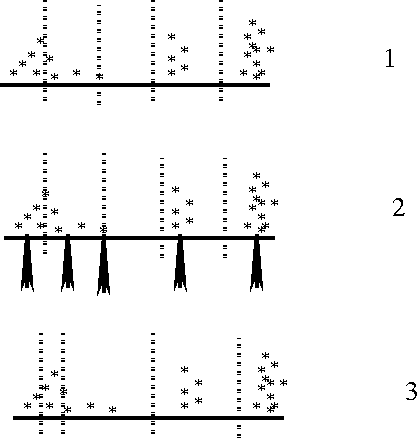
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) demonstrates a single iteration of this approach.
Steps 1-3 are repeated until the solution no longer changes significantly.
demonstrates a single iteration of this approach.
Steps 1-3 are repeated until the solution no longer changes significantly.
ref
Figure 1
In step 1, the data is dividing into cells. In step 2, the average
of each cell is calculated. In the third step new cell boundaries
are calculated between the centroids. If a cell contains no
points, the cell is removed.
|
|  |

Lloyd's method is attempting to solve a non-linear problem
by an iterative scheme, so local minima can be
problematic.
To avoid prejudicing the solution
the initial model is often a random set of vectors. To solve the
problem, several methods have been developed Linde et al. (1980).
These methods often rely on replacing an empty cell by
splitting regions with high variance.
Clapp (2002) followed
a modified version of this approach for the velocity selection
problem.
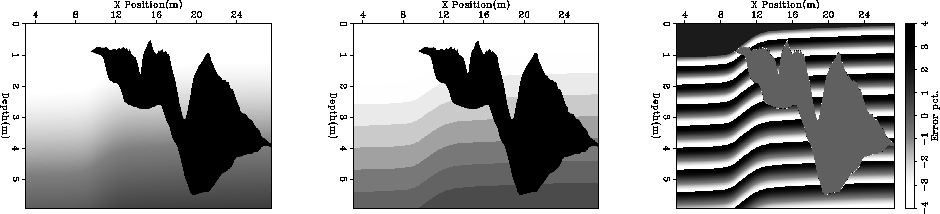
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a velocity model, the selected reference
velocities, and the percentage error between the two using
the methodology described in Clapp (2002). The methodology
proved effective in selecting appropriate reference velocities
with two noticeable drawbacks. At each depth step a new non-linear
estimate is performed. At some depths steps the solution
gets stuck in local-minima.
Note the striping in the right panel of Figure
shows a velocity model, the selected reference
velocities, and the percentage error between the two using
the methodology described in Clapp (2002). The methodology
proved effective in selecting appropriate reference velocities
with two noticeable drawbacks. At each depth step a new non-linear
estimate is performed. At some depths steps the solution
gets stuck in local-minima.
Note the striping in the right panel of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
In addition, the methodology will sometimes
pick too few reference velocities to adequately describe
a layer by getting stuck in a local minima.
Both of these problems can
be minimized by using as a starting solution the reference
velocities at the previous depth step and adding a random component
to the cell splitting. Figure
.
In addition, the methodology will sometimes
pick too few reference velocities to adequately describe
a layer by getting stuck in a local minima.
Both of these problems can
be minimized by using as a starting solution the reference
velocities at the previous depth step and adding a random component
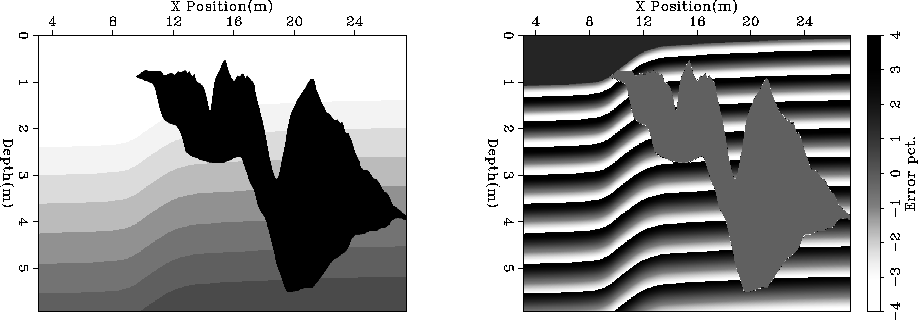
to the cell splitting. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the selected reference
velocities and the percentage error in the selected reference velocities.
shows the selected reference
velocities and the percentage error in the selected reference velocities.
error1
Figure 2 The left panel shows a velocity model from
a 2-D synthetic. The center panel shows the reference velocities selected
using the Lloyd's approach described in Clapp (2002). The right
panel shows the percent error between the selected reference velocity and
the the true velocity. Note the striping due to local minima.




 error2
error2
Figure 3 The left panel shows the selected
reference velocity using an improved selection scheme. The right
panel shows the error percentage error between the selected reference
and the true velocity. Note the reduced error compared to the right
panel of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.










Next: Extension to N-D
Up: R. Clapp: A modified
Previous: R. Clapp: A modified
Stanford Exploration Project
4/5/2006

![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) demonstrates a single iteration of this approach.
Steps 1-3 are repeated until the solution no longer changes significantly.
demonstrates a single iteration of this approach.
Steps 1-3 are repeated until the solution no longer changes significantly.

![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a velocity model, the selected reference
velocities, and the percentage error between the two using
the methodology described in Clapp (2002). The methodology
proved effective in selecting appropriate reference velocities
with two noticeable drawbacks. At each depth step a new non-linear
estimate is performed. At some depths steps the solution
gets stuck in local-minima.
Note the striping in the right panel of Figure
shows a velocity model, the selected reference
velocities, and the percentage error between the two using
the methodology described in Clapp (2002). The methodology
proved effective in selecting appropriate reference velocities
with two noticeable drawbacks. At each depth step a new non-linear
estimate is performed. At some depths steps the solution
gets stuck in local-minima.
Note the striping in the right panel of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
In addition, the methodology will sometimes
pick too few reference velocities to adequately describe
a layer by getting stuck in a local minima.
Both of these problems can
be minimized by using as a starting solution the reference
velocities at the previous depth step and adding a random component
to the cell splitting. Figure
.
In addition, the methodology will sometimes
pick too few reference velocities to adequately describe
a layer by getting stuck in a local minima.
Both of these problems can
be minimized by using as a starting solution the reference
velocities at the previous depth step and adding a random component
to the cell splitting. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the selected reference
velocities and the percentage error in the selected reference velocities.
shows the selected reference
velocities and the percentage error in the selected reference velocities.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.