We want to create a common azimuth volume, specifically the zero azimuth
volume, so we want to create a dataset where hy=0.
AMO provides a way to translate between different offsets.
We can create an operator ![]() that sums over hy volumes
that have been translated to hy=0 using AMO.
Unlike Clapp (2005a),
we will also sum over a small range of hx. This additional
summation allows for additional mixing of information in the
five-dimensional space.
We can define transforming from hx1,hy1 to hx2,hy2 using
AMO as Zhx1,hy1,hx2,hy2.
We can define our hx sampling interval as dhx, the number of samples
as nhx, and the first location as ohx. Similarly our sampling
hy is defined by nhy,ohy, and dhy. Given
that sums over hy volumes
that have been translated to hy=0 using AMO.
Unlike Clapp (2005a),
we will also sum over a small range of hx. This additional
summation allows for additional mixing of information in the
five-dimensional space.
We can define transforming from hx1,hy1 to hx2,hy2 using
AMO as Zhx1,hy1,hx2,hy2.
We can define our hx sampling interval as dhx, the number of samples
as nhx, and the first location as ohx. Similarly our sampling
hy is defined by nhy,ohy, and dhy. Given ![]() samples
we wish to sum over we can write an equation relating our domain m and
range d through
samples
we wish to sum over we can write an equation relating our domain m and
range d through
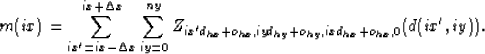 |
(1) |
Finally, we need to add in our regularization term.
Generally, after NMO, our data should be smooth
as a function of offset.
By applying a
derivative operator along
the offset axis we can emphasize this smoothness
and help fill in acquisition holes caused by
data irregularity. We can improve this estimate
even further by applying a derivative on cubes
that have been transformed to the same offset using
AMO![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif)
![]() .We can write our objective function as
.We can write our objective function as
| (2) |
| |
(3) |