Flip-flop interpolation

The most tractable problem for this data and also the most commonly shown interpolation result is increasing the number of shots by a factor of 2. This will result in a source distribution where the flip and flop shots for a given in-line position are both present. While the desired goal for this data is to increase the in-line source sampling by a factor of 3, interpolating by a factor of 2 does have the benefit of decreasing the cross-line density requirement by a factor of 2, and also results in having pairs of shots with relatively dense (25m) sampling in the cross-line direction. This is a big step up from the 200m between sail lines.

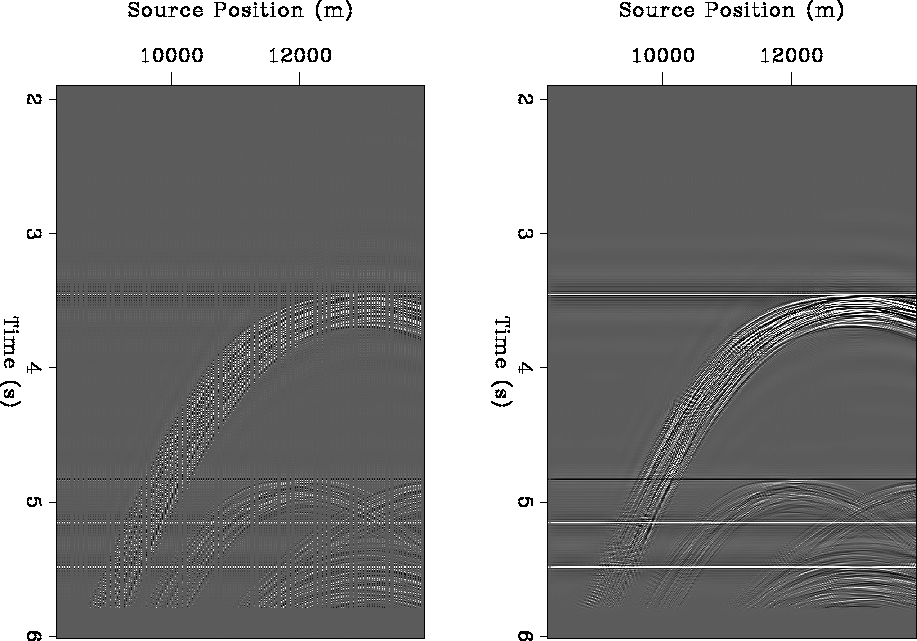
Results for an increase in shots by a factor of two are shown in Figure . The panel on the left corresponds to the input data, which is in this case a common receiver gather. The missing traces correspond to missing "flip" shots. The panel in the center of the figure corresponds to a 2D PEF-based interpolation, while the panel on the right corresponds to a 3D PEF-based interpolation, where the PEF is estimated along the receiver cable as well as across the source and time axes. There are only minimal differences between the 2D and 3D results. This is because the 2D result is actually quite good, and shows that an overly computationally intensive method is not necessary for this problem.

 

flipflopx2
Figure 2 Flip-flop interpolation of a common-receiver-section (offset=1250m). From left to right: original input common-receiver gather; result of 2D interpolation; result of 3D interpolation.

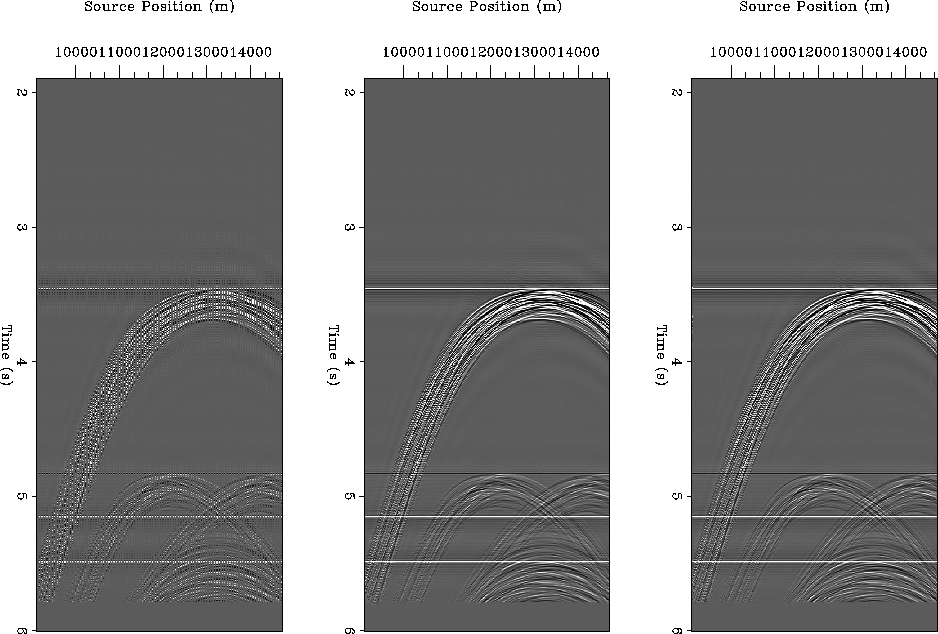
Now that the factor of 2 shot interpolation has been shown to be relatively insensitive to the dimensionality of the interpolation, this same test is repeated for increasing the shot sampling by a factor of 3, which would correspond to the ideal output. The results are shown in Figure . The interpolation is not nearly as good as for the case with the factor of 2. This is in part due to the increased expansion of the PEF coefficients that is required, and thus the approximation that the filter is scale-invariant becomes less valid.

 

flipflopx3
Figure 3 Flip-flop interpolation, factor of 3. From left to right: original input common-receiver gather; result of 2D interpolation.

Increasing the dimensionality of the interpolation in this case appears to have more effect than in the previous factor of 2 case.