




Next: Data Description
Up: Curry: Interpolating diffracted multiples
Previous: Introduction
Interpolation can be posed as a two-stage problem, where in the first
stage some statistics of the data are gathered, and in the second stage this
information is applied to fill in the missing data. In the case of
transform-based interpolation methods, the initial transform corresponds to the
gathering of information on existing data, and the second stage is the transform
back to the original, more densely-sampled space.
In terms of the prediction-error filter based interpolation used in this paper,
in the first stage an estimate of the data is made by creating a non-stationary
prediction-error filter (PEF) from the data by solving a linear least-squares
inverse problem,
| 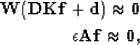 |
|
| (1) |
where 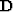 represents non-stationary convolution with the data,
represents non-stationary convolution with the data, 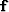 is
a non-stationary PEF,
is
a non-stationary PEF, 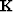 (a selector matrix) constrains the value of the
first filter coefficient to 1,
(a selector matrix) constrains the value of the
first filter coefficient to 1, 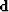 is a copy of the data,
is a copy of the data, 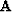 is a
regularization operator (a Laplacian operating over space) and
is a
regularization operator (a Laplacian operating over space) and  is a
trade-off parameter for the regularization. Solving this system will
create a smoothly varying non-stationary PEF that, when convolved with the data, will
ideally remove all coherent energy from the input data.
is a
trade-off parameter for the regularization. Solving this system will
create a smoothly varying non-stationary PEF that, when convolved with the data, will
ideally remove all coherent energy from the input data.
Once the PEF has been estimated, we can use it to constrain the missing
data by solving a second linear least-squares inverse problem,
| 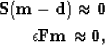 |
|
| (2) |
where 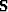 is a selector matrix which is 1 where data
is present and where it is not,
is a selector matrix which is 1 where data
is present and where it is not, 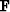 represents convolution with the
non-stationary PEF,
represents convolution with the
non-stationary PEF,  is now a trade-off parameter and
is now a trade-off parameter and 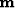 is the desired
model.
is the desired
model.
In order to interpolate by a factor of two, the coefficients of the PEF are
expanded so that the filter coefficients fall on known data. Once the PEF is
estimated, the filter is shrunk down to its original size and then used to interpolate.





Next: Data Description
Up: Curry: Interpolating diffracted multiples
Previous: Introduction
Stanford Exploration Project
4/5/2006