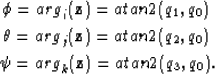Next: Quaternionic Transform
Up: Witten: Quaternion-based Signal Processing
Previous: Introduction
The set of hypercomplex numbers is defined as
| 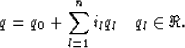 |
(1) |
Hypercomplex numbers
define a n+1-dimensional complex space with il orthonormal to im, for l
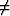 m. For all cases presented in this
paper l will be limited to 3. Such numbers are quaternions, which
can be represented as
q=q0+iq1+jq2+kq3, where i,j,k are imaginary numbers that
satisfying the following relations:
m. For all cases presented in this
paper l will be limited to 3. Such numbers are quaternions, which
can be represented as
q=q0+iq1+jq2+kq3, where i,j,k are imaginary numbers that
satisfying the following relations:
| 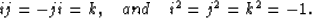 |
(2) |
Table 1:
The multiplication table for quaternion algebra.
| |
1 |
i |
j |
k |
| 1 |
1 |
i |
j |
k |
| i |
i |
-1 |
k |
-j |
| j |
j |
-k |
-1 |
i |
| k |
k |
j |
-i |
-1 |
The multiplication table for quaternion unit vectors is shown in
Table 1.
With these definitions, quaternionic addition between two quaternions,
q and p,
can be defined as
| 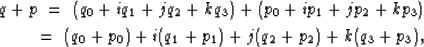 |
|
| (3) |
and multiplication as
| 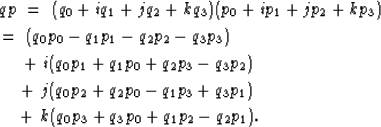 |
|
| |
| |
| |
| (4) |
Notice that multiplication in equation 4, is not
commutative due to the quaternionic algebra rules defined in table
1.
Quaternions are often separated into two parts, q0 and
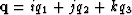 , respectively called the scalar and vector
part of the quaternion.
Using this definition, the conjugate of q,
, respectively called the scalar and vector
part of the quaternion.
Using this definition, the conjugate of q,  , is
, is
| 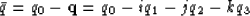 |
(5) |
and the norm of a quaternion is defined by
| 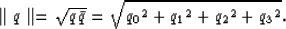 |
(6) |
It is useful to formulate a polar representation of the
quaternion, as this will be the primary notation throughout this
paper. For any complex number, 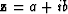 , the argument or
phase-angle is defined as atan2(b,a). If
, the argument or
phase-angle is defined as atan2(b,a). If  is written it
the form
is written it
the form 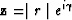 , then
, then 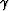 is the
phase (argument) of
is the
phase (argument) of  , denoted arg(
, denoted arg( )=
)=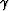 .Quaternions contain three complex subfields and, correspondingly, three
phases that are the projections onto the i, j, or k-complex plane,
.Quaternions contain three complex subfields and, correspondingly, three
phases that are the projections onto the i, j, or k-complex plane,
| 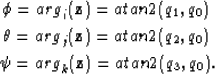 |
(7) |
| (8) |
| (9) |
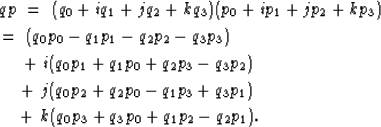
![]() , the argument or
phase-angle is defined as atan2(b,a). If
, the argument or
phase-angle is defined as atan2(b,a). If ![]() is written it
the form
is written it
the form ![]() , then
, then ![]() is the
phase (argument) of
is the
phase (argument) of ![]() , denoted arg(
, denoted arg(![]() )=
)=![]() .Quaternions contain three complex subfields and, correspondingly, three
phases that are the projections onto the i, j, or k-complex plane,
.Quaternions contain three complex subfields and, correspondingly, three
phases that are the projections onto the i, j, or k-complex plane,