Next: Conclusion and Discussion
Up: Wang: Imaging
Previous: [8] The convergence of
Beylkin (1985) gave a formula for estimating the (locations of) discontinuities of the unknown function describing the medium, rather than for estimating the function itself. The generalized back-projection operator R* dual to the generalized Radon transform R is defined as
| 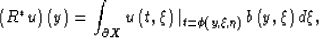 |
(94) |
where 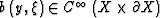 is a weighting function which is a smooth, non-negative function on
is a weighting function which is a smooth, non-negative function on 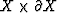 . It is defined as
. It is defined as
| 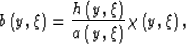 |
(95) |
where 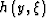 is a Jacobian determinant,
is a Jacobian determinant, 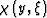 is a cut-off function,
is a cut-off function, 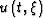 can be regarded as a generalized projection, which is the observed scattered wavefield on the surface.
With the help of a Fourier integral operator (FIO), the following formula can be obtained:
can be regarded as a generalized projection, which is the observed scattered wavefield on the surface.
With the help of a Fourier integral operator (FIO), the following formula can be obtained:
| 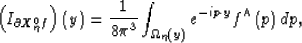 |
(96) |
where 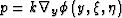 , which is the direction normal to the reflector at the imaging point.
, which is the direction normal to the reflector at the imaging point.
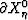 is the limited aperture on the surface, and
is the limited aperture on the surface, and 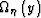 is the corresponding limited aperture near the imaging point. And
is the corresponding limited aperture near the imaging point. And 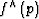 is the Fourier transform of the object function.
From Theorem 1 in Beylkin (1985), the inverse transform of the Fourier transform of the object function,
is the Fourier transform of the object function.
From Theorem 1 in Beylkin (1985), the inverse transform of the Fourier transform of the object function, 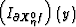 , approximately equals the generalized back-projection defined by equation (94).
Clearly, if the observation aperture
, approximately equals the generalized back-projection defined by equation (94).
Clearly, if the observation aperture 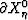 or
or 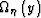 is unlimited, the discontinuities of the object function can be accurately estimated with equation (94) under some assumptions.
That is to say, true-amplitude imaging can be theoretically implemented under some conditions. Here, we point that the relative true-amplitude imaging can be obtained in practice even though the observation aperture is always limited.
Equation (96) can be considered as a summation. If the distribution of the Fourier transform of the object function on
is unlimited, the discontinuities of the object function can be accurately estimated with equation (94) under some assumptions.
That is to say, true-amplitude imaging can be theoretically implemented under some conditions. Here, we point that the relative true-amplitude imaging can be obtained in practice even though the observation aperture is always limited.
Equation (96) can be considered as a summation. If the distribution of the Fourier transform of the object function on 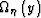 is even, and the range of the distribution is the same at every imaging point (or scattering point), the summation will be same. Even though the summation is not the true estimation for the discontinuities of the object function, the relative relation among these discontinuities at each imaging point is correct. This is the essence of the relative true-amplitude imaging or true-amplitude imaging.
What prevent relative true-amplitude imaging? Missing data and limited aperture are the two main factors, assuming that the the back-projection operator is suitable. Beylkin (1985); Bleistein and Stockwell (2001); Zhang (2004) discussed how to construct a suitable back-projection operator or true-amplitude imaging operator.
From the above point, we can further understand the meaning of the illumination analysis. The objective of the illumination analysis is to make clear how to map the observations on
is even, and the range of the distribution is the same at every imaging point (or scattering point), the summation will be same. Even though the summation is not the true estimation for the discontinuities of the object function, the relative relation among these discontinuities at each imaging point is correct. This is the essence of the relative true-amplitude imaging or true-amplitude imaging.
What prevent relative true-amplitude imaging? Missing data and limited aperture are the two main factors, assuming that the the back-projection operator is suitable. Beylkin (1985); Bleistein and Stockwell (2001); Zhang (2004) discussed how to construct a suitable back-projection operator or true-amplitude imaging operator.
From the above point, we can further understand the meaning of the illumination analysis. The objective of the illumination analysis is to make clear how to map the observations on 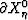 to
to 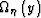 . If, on
. If, on 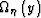 , the distribution of the Fourier transform of the object function is even, and the range of the distribution is the same at every imaging point (or scattering point), then relative true-amplitude imaging can be achieved.
It is worth to point out that the distribution should be symmetrical about the normal to the reflector at the imaging point.
true_amplitude_and_illumination
, the distribution of the Fourier transform of the object function is even, and the range of the distribution is the same at every imaging point (or scattering point), then relative true-amplitude imaging can be achieved.
It is worth to point out that the distribution should be symmetrical about the normal to the reflector at the imaging point.
true_amplitude_and_illumination
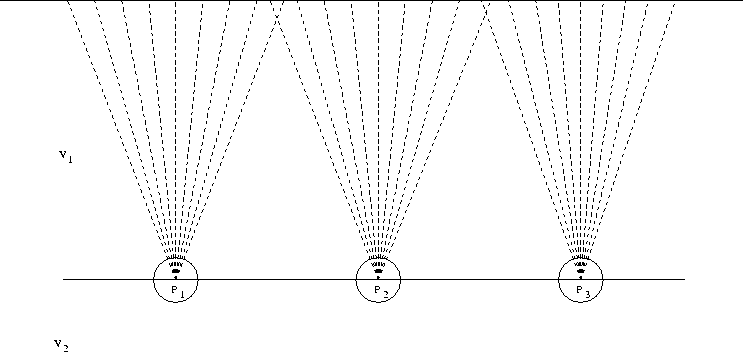
Figure 6 the possibility interpretation of the relative true-amplitude imaging in the case of simple medium structure.




 true_amplitude_and_illum22
true_amplitude_and_illum22
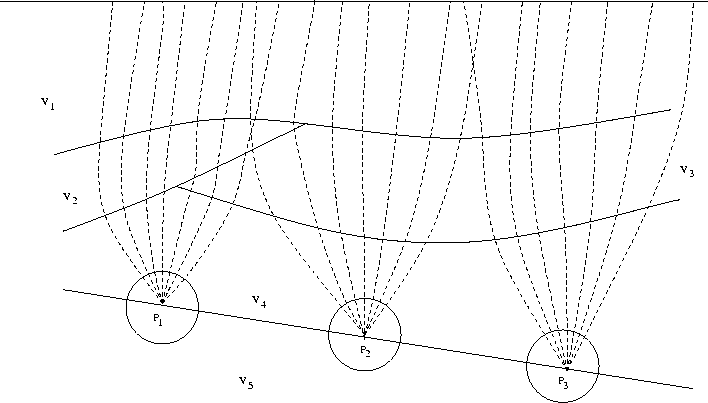
Figure 7 the possibility interpretation of the relative true-amplitude imaging in the case of complex medium structure.










Next: Conclusion and Discussion
Up: Wang: Imaging
Previous: [8] The convergence of
Stanford Exploration Project
11/1/2005