




Next: [2] The matrix expression
Up: Aspects of Linearized migration/inversion
Previous: Aspects of Linearized migration/inversion
The forward and backward propagations of the wavefield play a key role in the migration/inversion imaging. The Helmholtz equation is commonly used for depicting wave propagation in acoustic media. Based on it, I derive the formulas for traveltime and amplitude calculation corresponding to the main seismic wave energy.
In spherical coordinates, the Helmholtz equation is of the following form:
| 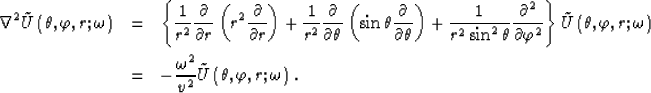 |
|
| (51) |
Equation (51) can be rewritten as
| 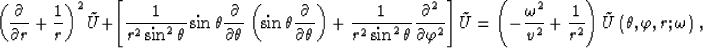 |
(52) |
The outward one-way wave equation can be derived from equation (52) as follows:
| ![\begin{displaymath}
\left(\frac{\partial }{\partial r} +\frac{1}{r}\right)\tilde...
...}} \right] }\tilde{U}\left( \theta, \varphi, r; \omega \right),\end{displaymath}](img122.gif) |
(53) |
where  is defined as
is defined as 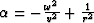 . Equation (53) can be expanded as
. Equation (53) can be expanded as
| ![\begin{displaymath}
\left(\frac{\partial }{\partial r} +\frac{1}{r}\right)\tilde...
...}} \right] }\tilde{U}\left( \theta, \varphi, r; \omega \right),\end{displaymath}](img122.gif) |
(54) |
where a and b are the optimal coefficients.
Then, equation (54) is split into two equations:
| 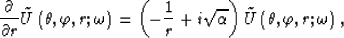 |
(55) |
| ![\begin{eqnarray}
&&\left\lbrace 1+\frac{b}{\alpha r^{2}\sin^{2} \theta }
\left[...
...2}}
\right]
\tilde{U}\left( \theta, \varphi, r; \omega \right) .\end{eqnarray}](img126.gif) |
|
| (56) |
Obviously, equation (55) can be solved analytically, and equation (56) can be solved by finite-differences.
The finite-difference scheme can be written in the following form:
| ![\begin{displaymath}
\left[I-\left( \alpha_{\theta}-i\beta_{\theta}\right) T_{\th...
...i\beta_{\varphi}\right) T_{\theta} \right]\tilde{U}^{n}_{i,j} ,\end{displaymath}](img127.gif) |
(57) |
where 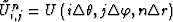 ,
, 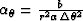 ,
, 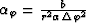 ,
, 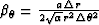 and
and 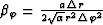 .The one-way wave extrapolation in the spherical coordinate system can be implemented by solving equation (55) and (57) in the frequency-space domain. The traveltime and amplitude corresponding to the maximum energy can be picked out in the frequency domain or time domain.
With the picked traveltime and amplitude, we carried out a 3D integral prestack depth migration which gave a high-quality imaging result Huazhong (2003). This demonstrates that the method can be used for constructing the Green's functions in the migration/inversion imaging.
.The one-way wave extrapolation in the spherical coordinate system can be implemented by solving equation (55) and (57) in the frequency-space domain. The traveltime and amplitude corresponding to the maximum energy can be picked out in the frequency domain or time domain.
With the picked traveltime and amplitude, we carried out a 3D integral prestack depth migration which gave a high-quality imaging result Huazhong (2003). This demonstrates that the method can be used for constructing the Green's functions in the migration/inversion imaging.





Next: [2] The matrix expression
Up: Aspects of Linearized migration/inversion
Previous: Aspects of Linearized migration/inversion
Stanford Exploration Project
11/1/2005
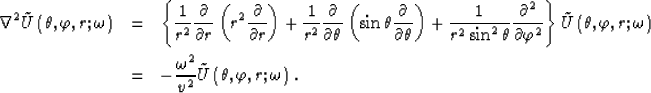
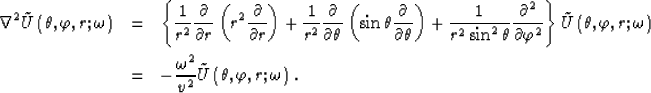
![\begin{eqnarray}
&&\left\lbrace 1+\frac{b}{\alpha r^{2}\sin^{2} \theta }
\left[...
...2}}
\right]
\tilde{U}\left( \theta, \varphi, r; \omega \right) .\end{eqnarray}](img126.gif)