




Next: Geometric interpretation of the
Up: Least-squares solution of the
Previous: Inversion of a 22
Using the results above, the least-squares estimate of
 in equation (
in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is derived.
Assuming that
) is derived.
Assuming that 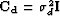 , the fitting goal is
, the fitting goal is
| 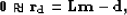 |
(97) |
with 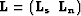 and
and 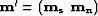 .The normal equations are given by
.The normal equations are given by
| 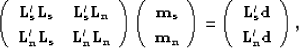 |
(98) |
where 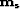 and
and 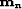 are the unknowns.
The least-square estimate
are the unknowns.
The least-square estimate 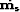 of
of 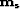 can be
derived from the bottom row of equation (
can be
derived from the bottom row of equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
The least-square estimate
).
The least-square estimate 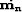 of
of 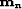 can be
derived from the top row of equation (
can be
derived from the top row of equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
We have, then,
).
We have, then,
| 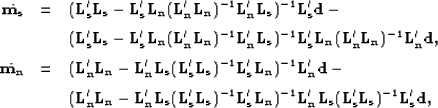 |
(99) |
| |
| (100) |
| |
which can be simplified as follows:
| 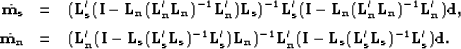 |
(101) |
| (102) |
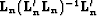 is the coherent noise resolution matrix,
whereas
is the coherent noise resolution matrix,
whereas 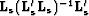 is the signal resolution
matrix Tarantola (1987).
Denoting
is the signal resolution
matrix Tarantola (1987).
Denoting 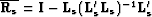 and
and 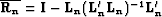 yields the following simplified expression for
yields the following simplified expression for 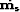 and
and
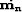 :
:
| 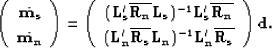 |
(103) |
By property of the resolution operators, 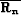 and
and
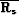 perform noise and signal filtering, i.e.,
perform noise and signal filtering, i.e.,
| 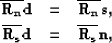 |
(104) |
if the noise and signal are well predicted by the noise
and signal modeling operators. Nemeth (1996) demonstrates
that the inverse of the Hessian in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
is well conditioned if the noise and signal operators are orthogonal,
meaning that they predict distinct parts of the model space without
overlapping. If overlapping occurs, a model regularization term can
improve the signal/noise separation.
)
is well conditioned if the noise and signal operators are orthogonal,
meaning that they predict distinct parts of the model space without
overlapping. If overlapping occurs, a model regularization term can
improve the signal/noise separation.





Next: Geometric interpretation of the
Up: Least-squares solution of the
Previous: Inversion of a 22
Stanford Exploration Project
5/5/2005
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is derived.
Assuming that
) is derived.
Assuming that ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
The least-square estimate
).
The least-square estimate ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
We have, then,
).
We have, then,
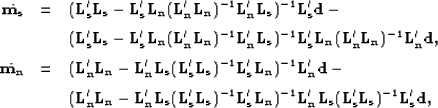
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
is well conditioned if the noise and signal operators are orthogonal,
meaning that they predict distinct parts of the model space without
overlapping. If overlapping occurs, a model regularization term can
improve the signal/noise separation.
)
is well conditioned if the noise and signal operators are orthogonal,
meaning that they predict distinct parts of the model space without
overlapping. If overlapping occurs, a model regularization term can
improve the signal/noise separation.