




Next: Least-squares solution of the
Up: Algorithm for minimizing the
Previous: An efficient algorithm for
So far I have introduced a general method for solving nonlinear
problems. In this section I show how this algorithm can be used when
the Huber function is utilized for measuring the data misfit. In fact,
we only need to derive the gradient of the objective function in equation
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). The gradient can be written in the following
compact form Li and Swetist (1998):
). The gradient can be written in the following
compact form Li and Swetist (1998):
| 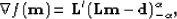 |
(84) |
where 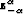 is a vector with ith component
is a vector with ith component
| 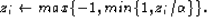 |
(85) |
A last difficulty arises in the choice of the threshold
 in equation (
in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
This value remains constant during the iterations.
).
This value remains constant during the iterations.
 is also the only parameter to choose a priori for different
problems. I have not derived any analytical expression for
is also the only parameter to choose a priori for different
problems. I have not derived any analytical expression for  , but
based on previous works with IRLS methods Darche (1989),
it seems that
, but
based on previous works with IRLS methods Darche (1989),
it seems that
| 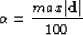 |
(86) |
is a good practical choice. Another possible solution is to set  at
the 98-th percentile of the data (Claerbout, 2000, Personal
communication).
at
the 98-th percentile of the data (Claerbout, 2000, Personal
communication).





Next: Least-squares solution of the
Up: Algorithm for minimizing the
Previous: An efficient algorithm for
Stanford Exploration Project
5/5/2005
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). The gradient can be written in the following
compact form Li and Swetist (1998):
). The gradient can be written in the following
compact form Li and Swetist (1998):
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
This value remains constant during the iterations.
).
This value remains constant during the iterations.