




Next: Minimizing the Huber function
Up: Algorithm for minimizing the
Previous: The limited memory BFGS
The solver works as follows:
- 1.
- Choose
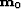 , l,
, l, 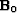 . Set k=0.
. Set k=0.
- 2.
- Compute
| 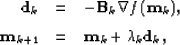 |
(79) |
| (80) |
where 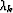 meets the Wolfe conditions.
meets the Wolfe conditions.
- 3.
- Let
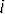 =min
=min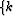 ,
, 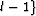 . Update
. Update 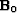
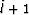 times using the pairs
times using the pairs
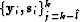 ,
i.e., let
,
i.e., let
| 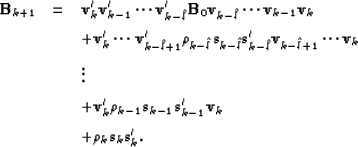 |
|
| |
| (81) |
| |
| (82) |
- 4.
- Set k=k+1 and go to 2 if the residual power is not small enough.
The update 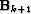 is not formed explicitly; instead we compute
is not formed explicitly; instead we compute
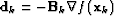 with an iterative formula
Nocedal (1980). Liu and Nocedal (1989) propose scaling the initial
symmetric positive definite
with an iterative formula
Nocedal (1980). Liu and Nocedal (1989) propose scaling the initial
symmetric positive definite 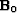 at each iteration as follows:
at each iteration as follows:
| 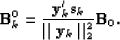 |
(83) |
This scaling greatly improves the performances of the method.
Liu and Nocedal (1989) show that the storage limit for large-scale problems
has little effects.
A common choice for l is l=5. In practice, the initial guess
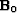 for the Hessian is the identity matrix
for the Hessian is the identity matrix 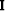 ;
then it might be scaled as proposed in equation (
;
then it might be scaled as proposed in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). The
nonlinear solver as detailed in the previous algorithm converges to
a local minimizer
). The
nonlinear solver as detailed in the previous algorithm converges to
a local minimizer 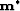 of
of 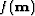 .
.





Next: Minimizing the Huber function
Up: Algorithm for minimizing the
Previous: The limited memory BFGS
Stanford Exploration Project
5/5/2005
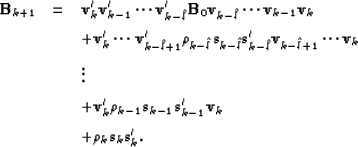
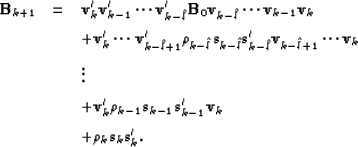
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). The
nonlinear solver as detailed in the previous algorithm converges to
a local minimizer
). The
nonlinear solver as detailed in the previous algorithm converges to
a local minimizer