




Next: An efficient algorithm for
Up: Algorithm for minimizing the
Previous: A quasi-Newton method for
Nocedal (1980) derives a technique that partially solves the storage
problem caused by the BFGS update. Instead of keeping all
the  and
and 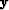 from the past
iterations, we update the Hessian using the information
from the l previous iterations, where l is given by the end-user.
This implies that when the number of iterations is smaller than l, we
have the usual BFGS update, and when it is larger than l, we have
a limited memory BFGS (L-BFGS) update.
from the past
iterations, we update the Hessian using the information
from the l previous iterations, where l is given by the end-user.
This implies that when the number of iterations is smaller than l, we
have the usual BFGS update, and when it is larger than l, we have
a limited memory BFGS (L-BFGS) update.
I give the updating formulas of the Hessian as presented
by Nocedal (1980). First, we define
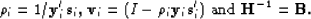
As described above, when k, the iteration number, obeys 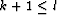 ,
where l is the storage limit, we have the BFGS update
,
where l is the storage limit, we have the BFGS update
| 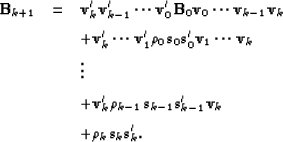 |
|
| |
| (75) |
| |
| |
For k+1 > l we have the limited memory update
| 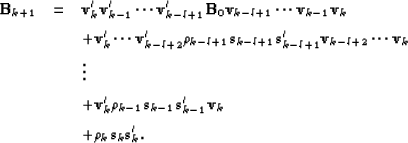 |
|
| |
| (76) |
| |
| |
These equations show how the update of the Hessian is calculated.
Usually the L-BFGS method is implemented with a line search for the
step length 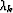 to ensure a
sufficient decrease of the misfit function.
Convergence properties of the L-BFGS method are guaranteed if
to ensure a
sufficient decrease of the misfit function.
Convergence properties of the L-BFGS method are guaranteed if
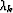 in equation (
in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) satisfies the Wolfe
conditions Kelley (1999):
) satisfies the Wolfe
conditions Kelley (1999):
| 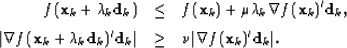 |
(77) |
| (78) |
 and
and 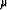 are constants to be chosen a priori and
are constants to be chosen a priori and
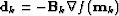 . For
. For  and
and 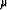 we set
we set 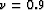 and
and 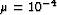 as proposed by
Liu and Nocedal (1989). Equation (
as proposed by
Liu and Nocedal (1989). Equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is a
sufficient decrease condition that all line search algorithms must
satisfy. Equation (
) is a
sufficient decrease condition that all line search algorithms must
satisfy. Equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is a curvature condition. The
line search algorithm has to be carefully designed since it absorbs
most of the computing time. I programmed a line search based on the
More and Thuente (1994) method. Because the line search is time
consuming, the step length
) is a curvature condition. The
line search algorithm has to be carefully designed since it absorbs
most of the computing time. I programmed a line search based on the
More and Thuente (1994) method. Because the line search is time
consuming, the step length 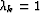 is always
tested first. This procedure saves a lot of computing time
and is also recommended by Liu and Nocedal (1989). I now give the
algorithm used to minimize any objective function involving nonlinear
problems.
is always
tested first. This procedure saves a lot of computing time
and is also recommended by Liu and Nocedal (1989). I now give the
algorithm used to minimize any objective function involving nonlinear
problems.





Next: An efficient algorithm for
Up: Algorithm for minimizing the
Previous: A quasi-Newton method for
Stanford Exploration Project
5/5/2005
![]()
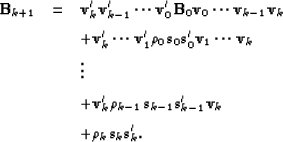
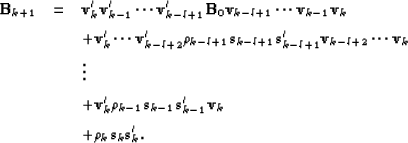
![]() to ensure a
sufficient decrease of the misfit function.
Convergence properties of the L-BFGS method are guaranteed if
to ensure a
sufficient decrease of the misfit function.
Convergence properties of the L-BFGS method are guaranteed if
![]() in equation (
in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) satisfies the Wolfe
conditions Kelley (1999):
) satisfies the Wolfe
conditions Kelley (1999):
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is a
sufficient decrease condition that all line search algorithms must
satisfy. Equation (
) is a
sufficient decrease condition that all line search algorithms must
satisfy. Equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is a curvature condition. The
line search algorithm has to be carefully designed since it absorbs
most of the computing time. I programmed a line search based on the
More and Thuente (1994) method. Because the line search is time
consuming, the step length
) is a curvature condition. The
line search algorithm has to be carefully designed since it absorbs
most of the computing time. I programmed a line search based on the
More and Thuente (1994) method. Because the line search is time
consuming, the step length