




Next: Preconditioning for accelerated convergence
Up: Interpolation of bathymetry data
Previous: Introduction
Now, a formulation of the regridding problem is developed.
Let 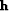 be an abstract vector containing as components the
water depth over a 2-D spatial mesh and
be an abstract vector containing as components the
water depth over a 2-D spatial mesh and 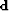 be an abstract
vector whose successive components represent depth along the vessel tracks.
One way to grid irregular data is to minimize the length
of the residual vector
be an abstract
vector whose successive components represent depth along the vessel tracks.
One way to grid irregular data is to minimize the length
of the residual vector 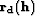
| 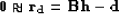 |
(34) |
where 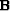 is a 2-D linear interpolation operator
and
is a 2-D linear interpolation operator
and 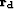 is the data residual. Note that sinc or spline
interpolants could be used as well, but a simple linear
interpolation operator is chosen to focus the analysis on the noise
attenuation problem only.
This fitting goal simply requires that the gridded data
is the data residual. Note that sinc or spline
interpolants could be used as well, but a simple linear
interpolation operator is chosen to focus the analysis on the noise
attenuation problem only.
This fitting goal simply requires that the gridded data 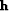 take on appropriate
values where the data
take on appropriate
values where the data 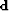 was collected. The bin size is 60 by
50 meters so that the number of data-points per bin is roughly
constant and the aspect ratio of the lake is preserved in the number
of samples in the east-west and north-south directions.
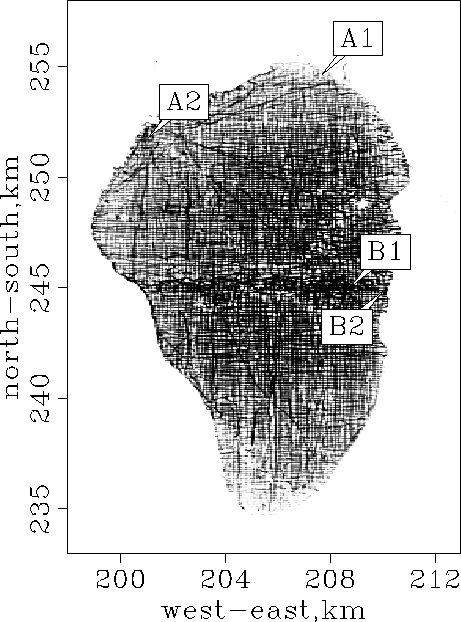
A simple binning (without interpolation or inversion) of the raw data (Figure
was collected. The bin size is 60 by
50 meters so that the number of data-points per bin is roughly
constant and the aspect ratio of the lake is preserved in the number
of samples in the east-west and north-south directions.
A simple binning (without interpolation or inversion) of the raw data (Figure
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is shown in Figure
) is shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . Note
that the north points to the top of the map in Figure
. Note
that the north points to the top of the map in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
A coarser mesh would avoid the empty bins but lose resolution.
As we refine the mesh for more detail, the number of empty bins grows
as does the care needed in devising a technique for filling them.
The black lines in Figure
.
A coarser mesh would avoid the empty bins but lose resolution.
As we refine the mesh for more detail, the number of empty bins grows
as does the care needed in devising a technique for filling them.
The black lines in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) are the ship
tracks. Notice that some data points are outside the contour of the
water. These must represent navigation errors.
fig1b
are the ship
tracks. Notice that some data points are outside the contour of the
water. These must represent navigation errors.
fig1b
Figure 2 Simple binning of the
raw data in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The ship tracks and empty
bins are visible and need to be accounted for in the inversion
process. The north points to the top.
. The ship tracks and empty
bins are visible and need to be accounted for in the inversion
process. The north points to the top.





Unless data is collected everywhere on a very fine mesh, and depending on how
the grid is parameterized, the regridding may leave holes on
the mesh. We can eliminate the holes by adding some regularization, like
| 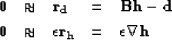 |
(35) |
where 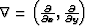 and
and 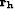 is the model space
residual. We then minimize the misfit function
is the model space
residual. We then minimize the misfit function
| 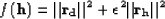 |
(36) |
to estimate the interpolated map of the lake. The second term
in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) becomes Laplace's equation.
In theory Tarantola (1987), the regularization operator
(squared) should be the inverse model covariance
operator given an a-priori model
) becomes Laplace's equation.
In theory Tarantola (1987), the regularization operator
(squared) should be the inverse model covariance
operator given an a-priori model 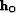 . Since we do not have
any a-priori model, I simply chose the gradient operator
. Since we do not have
any a-priori model, I simply chose the gradient operator 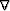 as a way of saying that the bottom of the lake is smooth.
However, as pointed out by Harlan (1995), the regularization and the data
fitting goal in equation (
as a way of saying that the bottom of the lake is smooth.
However, as pointed out by Harlan (1995), the regularization and the data
fitting goal in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) contradict each other. One
equation tends to add details in the final map whereas the second one
(the regularization) tends to smooth it. We can more easily balance
these two goals by preconditioning the problem
Fomel (2001).
) contradict each other. One
equation tends to add details in the final map whereas the second one
(the regularization) tends to smooth it. We can more easily balance
these two goals by preconditioning the problem
Fomel (2001).
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is shown in Figure
) is shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . Note
that the north points to the top of the map in Figure
. Note
that the north points to the top of the map in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
A coarser mesh would avoid the empty bins but lose resolution.
As we refine the mesh for more detail, the number of empty bins grows
as does the care needed in devising a technique for filling them.
The black lines in Figure
.
A coarser mesh would avoid the empty bins but lose resolution.
As we refine the mesh for more detail, the number of empty bins grows
as does the care needed in devising a technique for filling them.
The black lines in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) are the ship
tracks. Notice that some data points are outside the contour of the
water. These must represent navigation errors.
are the ship
tracks. Notice that some data points are outside the contour of the
water. These must represent navigation errors.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The ship tracks and empty
bins are visible and need to be accounted for in the inversion
process. The north points to the top.
. The ship tracks and empty
bins are visible and need to be accounted for in the inversion
process. The north points to the top.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) becomes Laplace's equation.
In theory Tarantola (1987), the regularization operator
(squared) should be the inverse model covariance
operator given an a-priori model
) becomes Laplace's equation.
In theory Tarantola (1987), the regularization operator
(squared) should be the inverse model covariance
operator given an a-priori model ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) contradict each other. One
equation tends to add details in the final map whereas the second one
(the regularization) tends to smooth it. We can more easily balance
these two goals by preconditioning the problem
Fomel (2001).
) contradict each other. One
equation tends to add details in the final map whereas the second one
(the regularization) tends to smooth it. We can more easily balance
these two goals by preconditioning the problem
Fomel (2001).