Introduction

In this problem, we are given depth sounding data from the Sea of Galilee. The Sea of Galilee is unique because it is a fresh-water lake below sea-level. It is connected to a transform fault system (Levant fault zone) along the eastern margin of the Mediterranean Sea. The ultimate goal is to produce not only a good map of the depth to bottom, but images useful for the purpose of identifying archaeological, geological, or geophysical details of the sea bottom. In particular, we hope to be able to identify some ancient shorelines around the lake and meaningful geological features inside the lake. The ancient shorelines could unravel early settlements of archaeological interest or old fishing ports.

The raw data (Figure ), irregularly distributed across the surface, are 132,044 triples, (x_i,y_i,z_i), where x_i ranges over about 12 km and where y_i ranges over about 20 km. The data need to be interpolated to a regular grid using inversion to facilitate the processing, such as noise removal, and also to create a map that can be easily analyzed for identifying artifacts and geology.

The pertinence of this dataset to our daily geophysical problems is three fold. First, we often have to do interpolation of seismic maps Britze (1998), potential field data Guspi and Introcaso (2000) or other measurements to compensate for the sparseness and irregularities of acquisition geometries. Second, as seen in the raw data in Figure , some noise bursts related to spurious electronic signals (glitches) and/or positioning errors need to be accounted for in the inversion scheme. This problem is common, for example, in tomography Bube and Langan (1997), deconvolution of noisy data Chapman and Barrodale (1983) and velocity analysis (Chapter ) where outliers can degrade the final model if we assume a gaussian distribution of the noise. Third, the final image of the Sea of Galilee will display the vessel tracks because the measurements on the lake were made on different days, with different weather and human conditions. We can directly link this problem to the goal of removing the acquisition footprint with 3-D seismic data Chemingui and Biondi (2002); Duijndam et al. (2000); Schuster and Liu (2001). Therefore, the interpolation of the data from the Sea of Galilee becomes a spiky noise and a coherent noise attenuation problem.

 

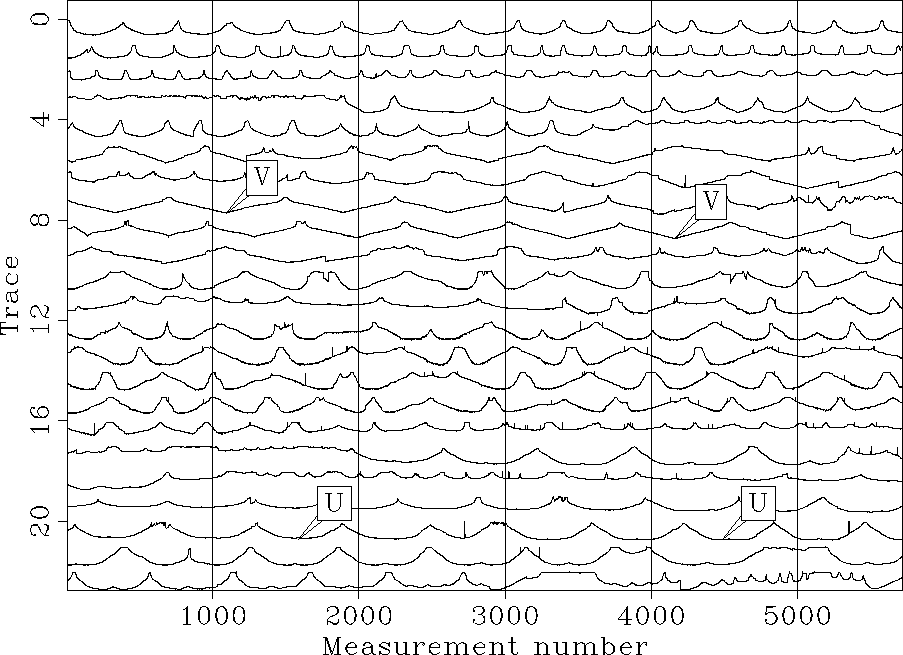
fig1
Figure 1 Depth of the Sea of Galilee along the vessel tracks. On one traverse across the lake, the depth record is ``u'' shaped. A few ``v'' shaped tracks result from vessel turn-arounds. All the points used for building the maps are shown here. Each point corresponds to one depth measurement inside the lake. Note that the input data are displayed as ``seismic traces'' for display purpose only. The long signal is broken into 23 strips of 5718 depth measurements. The horizontal axis corresponds to a measurement number. The depth appears as one long track although the surveying was done in several episodes that do not always continue the same track.

There is a long list of students at the Stanford Exploration Project who attempted to produce a satisfying map of the sea bottom. Fomel and Claerbout (1995) introduced the $\ell^1$ norm via Iteratively Reweighted Least Squares (IRLS) to eliminate the noise bursts present in the data. Recently, Brown (2001) attempted to remove acquisition tracks by estimating the systematic error between tracks at crossing points. Karpushin and Brown (2001) used a bank of prediction-error filters (PEFs) to whiten the residual along tracks. However, in most of these results, there is a loss of resolution that hampers our goal of seeing small features in the final image.

Techniques developed in the preceding Chapters, i.e., the Huber norm from Chapter and the modeling approach of Chapter , are both used to tackle the noise problems encountered with the mapping of this dataset. This data example also illustrates that the modeling of the tracks gives better results than filtering.