




Next: Conclusions
Up: Adaptive subtraction of multiples
Previous: Adaptive subtraction results
In this section I attenuate in the poststack domain
surface-related multiples with shaping filters
that I estimate with the  and
and  norm. These filters are
non-stationary. Figure
norm. These filters are
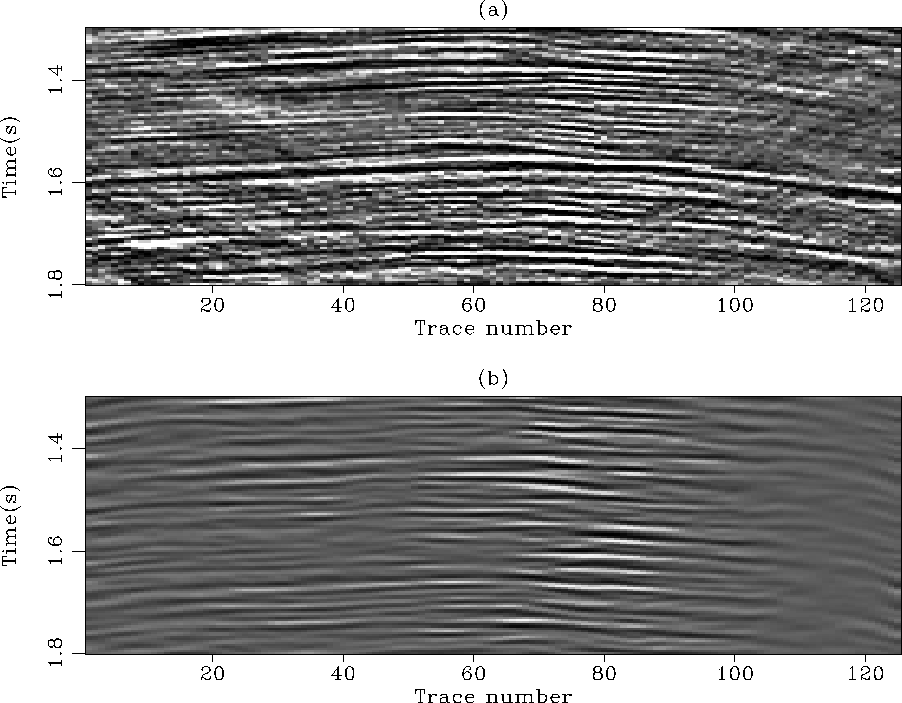
non-stationary. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a shows the multiple-infested data.
Figure
a shows the multiple-infested data.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b displays the multiple model computed with
a data-driven modeling approach Kelamis and Verschuur (2000). Note that for this
gather, the amplitude differences between the primaries and the multiples
are not very strong.
My goal is to illustrate the use of the
b displays the multiple model computed with
a data-driven modeling approach Kelamis and Verschuur (2000). Note that for this
gather, the amplitude differences between the primaries and the multiples
are not very strong.
My goal is to illustrate the use of the  norm
in a more general case when surface-related multiples are present in the data.
I specifically focus on the event at 1.6s in Figure
norm
in a more general case when surface-related multiples are present in the data.
I specifically focus on the event at 1.6s in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a.
This event is a primary that needs to be preserved by the subtraction procedure.
a.
This event is a primary that needs to be preserved by the subtraction procedure.
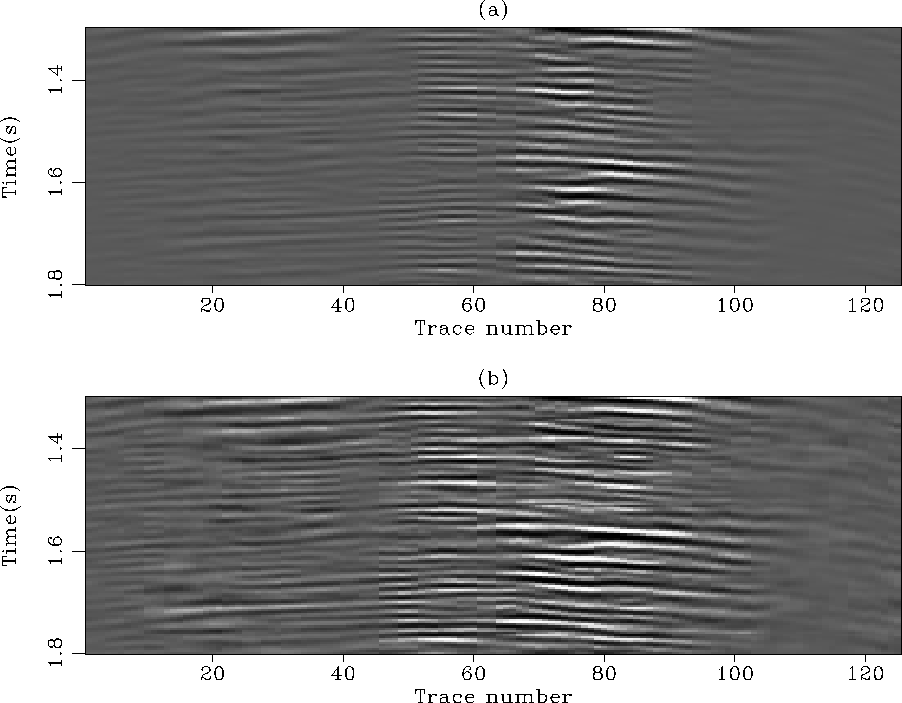
The amplitude of the primary at 1.6s is well preserved
with the  norm in Figure
norm in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a. Again,
a. Again,
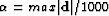 gave a satisfying result. However, the amplitude
of this primary is attenuated with the
gave a satisfying result. However, the amplitude
of this primary is attenuated with the  norm as displayed
in Figure
norm as displayed
in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b. Figure
b. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a comparison
between the subtracted multiples with the
shows a comparison
between the subtracted multiples with the  (Figure
(Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a)
and the
a)
and the  norm (Figure
norm (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b). I conclude that
the
b). I conclude that
the  norm tends to subtract too much energy.
norm tends to subtract too much energy.
win3
Figure 10 (a) Stack infested
with multiples. (b) The multiple model computed with the Delft modeling
approach. The subtraction is done poststack.




 win
win
Figure 11 (a) The estimated primaries
with  norm adaptive subtraction. (b) The estimated primaries
with
norm adaptive subtraction. (b) The estimated primaries
with  norm subtraction. The primary at 1.6s is very attenuated with
the
norm subtraction. The primary at 1.6s is very attenuated with
the  norm. The
norm. The  technique preserves its amplitude
better.
technique preserves its amplitude
better.




 win2
win2
Figure 12 (a) The estimated
multiples with the  norm subtraction. (b) The estimated multiples
with the
norm subtraction. (b) The estimated multiples
with the  norm subtraction. The
norm subtraction. The  norm tends to over-fit some
multiples that creates some leaking of primaries in the estimated noise.
norm tends to over-fit some
multiples that creates some leaking of primaries in the estimated noise.





This last example proves that the estimation of shaping
filters can always be done with the  norm. An advantage of
the inversion scheme with the Huber norm is that only one parameter
(i.e.,
norm. An advantage of
the inversion scheme with the Huber norm is that only one parameter
(i.e.,  ) controls the
) controls the  behavior. Thus it is easy
to switch from one norm to another.
Of course, it remains difficult to assert if the subtracted multiples
with the
behavior. Thus it is easy
to switch from one norm to another.
Of course, it remains difficult to assert if the subtracted multiples
with the  norm are more similar to the actual multiples than
the subtracted multiples with the
norm are more similar to the actual multiples than
the subtracted multiples with the  norm. This judgment is
only based on qualitative considerations for few known primary
reflectors that need to be preserved.
norm. This judgment is
only based on qualitative considerations for few known primary
reflectors that need to be preserved.





Next: Conclusions
Up: Adaptive subtraction of multiples
Previous: Adaptive subtraction results
Stanford Exploration Project
5/5/2005
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a. Again,
a. Again,
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b. Figure
b. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a comparison
between the subtracted multiples with the
shows a comparison
between the subtracted multiples with the ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a)
and the
a)
and the ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b). I conclude that
the
b). I conclude that
the ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a shows the multiple-infested data.
Figure
a shows the multiple-infested data.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b displays the multiple model computed with
a data-driven modeling approach Kelamis and Verschuur (2000). Note that for this
gather, the amplitude differences between the primaries and the multiples
are not very strong.
My goal is to illustrate the use of the
b displays the multiple model computed with
a data-driven modeling approach Kelamis and Verschuur (2000). Note that for this
gather, the amplitude differences between the primaries and the multiples
are not very strong.
My goal is to illustrate the use of the ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a.
This event is a primary that needs to be preserved by the subtraction procedure.
a.
This event is a primary that needs to be preserved by the subtraction procedure.
![]() norm in Figure
norm in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a. Again,
a. Again,
![]() gave a satisfying result. However, the amplitude
of this primary is attenuated with the
gave a satisfying result. However, the amplitude
of this primary is attenuated with the ![]() norm as displayed
in Figure
norm as displayed
in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b. Figure
b. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a comparison
between the subtracted multiples with the
shows a comparison
between the subtracted multiples with the ![]() (Figure
(Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a)
and the
a)
and the ![]() norm (Figure
norm (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b). I conclude that
the
b). I conclude that
the ![]() norm tends to subtract too much energy.
norm tends to subtract too much energy.

![]() norm. An advantage of
the inversion scheme with the Huber norm is that only one parameter
(i.e.,
norm. An advantage of
the inversion scheme with the Huber norm is that only one parameter
(i.e., ![]() ) controls the
) controls the ![]() behavior. Thus it is easy
to switch from one norm to another.
Of course, it remains difficult to assert if the subtracted multiples
with the
behavior. Thus it is easy
to switch from one norm to another.
Of course, it remains difficult to assert if the subtracted multiples
with the ![]() norm are more similar to the actual multiples than
the subtracted multiples with the
norm are more similar to the actual multiples than
the subtracted multiples with the ![]() norm. This judgment is
only based on qualitative considerations for few known primary
reflectors that need to be preserved.
norm. This judgment is
only based on qualitative considerations for few known primary
reflectors that need to be preserved.