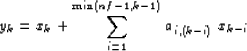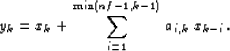Next: Filter estimation
Up: Estimation of nonstationary PEFs
Previous: Estimation of nonstationary PEFs
I call  the convolution or combination operator with a bank of
non-stationary filters. For the non-stationary convolution, the
filters are in the column of
the convolution or combination operator with a bank of
non-stationary filters. For the non-stationary convolution, the
filters are in the column of  (one filter corresponds to one
point in the input space) whereas for the non-stationary
combination, the filters lie in the rows of
(one filter corresponds to one
point in the input space) whereas for the non-stationary
combination, the filters lie in the rows of 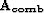 (one filter corresponds
to one point in the output space). For the convolution matrix,
I define ai,j as the ith coefficient of the filter for the jth
data point in the input space. For the combination matrix, I define
ai,j as the jth coefficient of the filter for the ith
data point in the output space. Therefore, for the non-stationary convolution we have
(one filter corresponds
to one point in the output space). For the convolution matrix,
I define ai,j as the ith coefficient of the filter for the jth
data point in the input space. For the combination matrix, I define
ai,j as the jth coefficient of the filter for the ith
data point in the output space. Therefore, for the non-stationary convolution we have
|  |
(120) |
and for the non-stationary combination we have
|  |
(121) |
The size of both matrices is 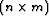 where n is the size of
an output vector (
where n is the size of
an output vector ( ) and m the size of an input vector
(
) and m the size of an input vector
(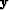 ) if
) if
| 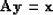 |
(122) |
The helical boundary conditions allow to generalize this
1-D convolution to higher dimensions. We can rewrite equation
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) for the convolution as follows:
) for the convolution as follows:
| 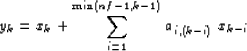 |
(123) |
where nf is the number of filter coefficients, and for the
combination
| 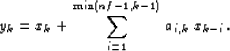 |
(124) |
In the next section, I show how the non-stationary PEFs are estimated.





Next: Filter estimation
Up: Estimation of nonstationary PEFs
Previous: Estimation of nonstationary PEFs
Stanford Exploration Project
5/5/2005



![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) for the convolution as follows:
) for the convolution as follows: