Next: Conclusion
Up: Sen and Biondi: COMAZ-AN
Previous: Error analysis
In this section, we compare the 3-D impulse responses of the anisotropic Common Azimuth migration operator with the corresponding isotropic one. For this paper, we consider impulse responses for elliptical anisotropy only. The vertical P wave velocity in the medium is 2000 m/s. The anisotropic parameters  and
and  are both equal to 0.15. Figures
are both equal to 0.15. Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
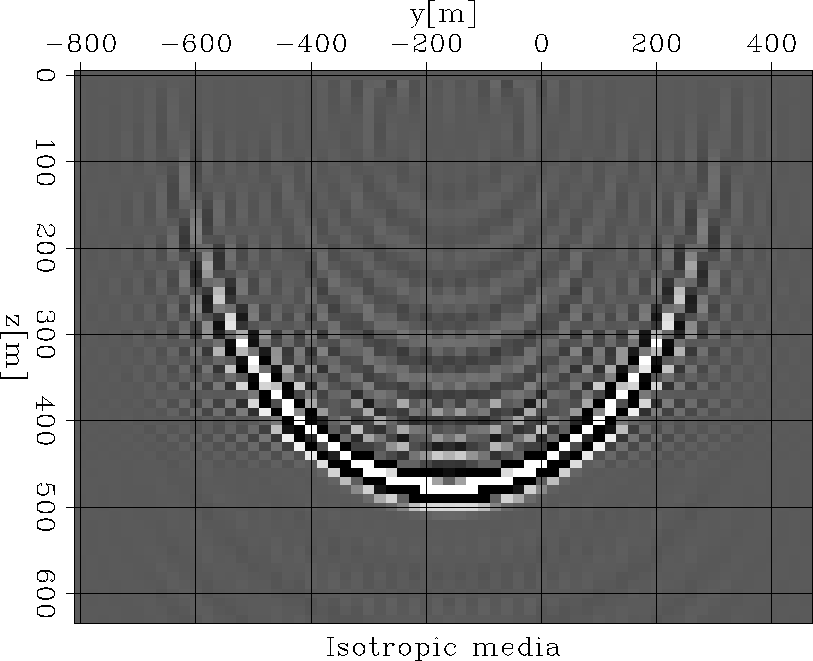
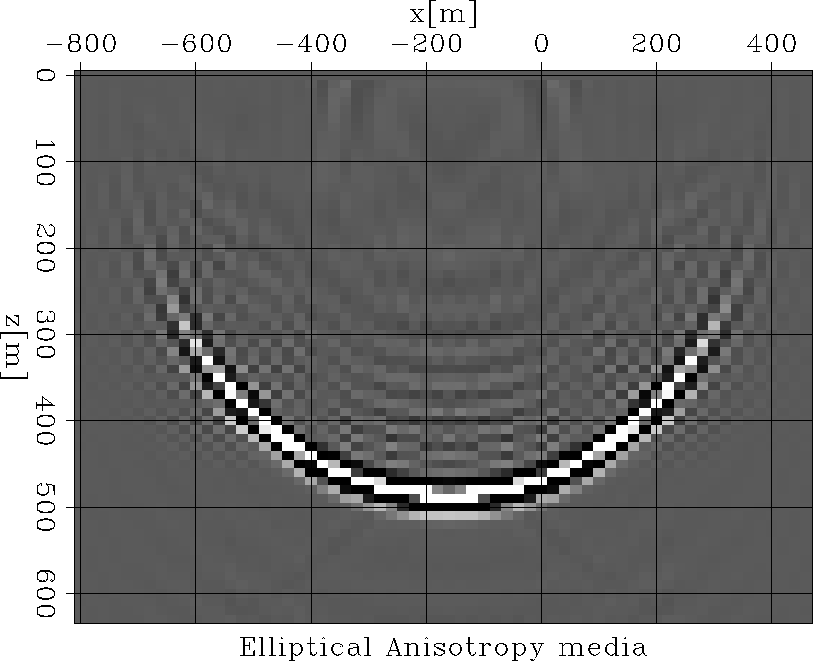
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) show in-line sections of the 3-D impulse responses for elliptically anisotropic and isotropic media respectively. These figures clearly show the difference of incorporating anisotropy into the Common Azimuth downward continuation operator, especially for energy propagating at moderate to steep angles.
Figures
show in-line sections of the 3-D impulse responses for elliptically anisotropic and isotropic media respectively. These figures clearly show the difference of incorporating anisotropy into the Common Azimuth downward continuation operator, especially for energy propagating at moderate to steep angles.
Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) show cross-line sections of the 3-D impulse responses for elliptically anisotropic and isotropic media respectively. Again it can be seen that there are significant differences for energy propagating at moderate to steep angles once anisotropy is incorporated into the Common Azimuth operator.
Finally, Figures
show cross-line sections of the 3-D impulse responses for elliptically anisotropic and isotropic media respectively. Again it can be seen that there are significant differences for energy propagating at moderate to steep angles once anisotropy is incorporated into the Common Azimuth operator.
Finally, Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
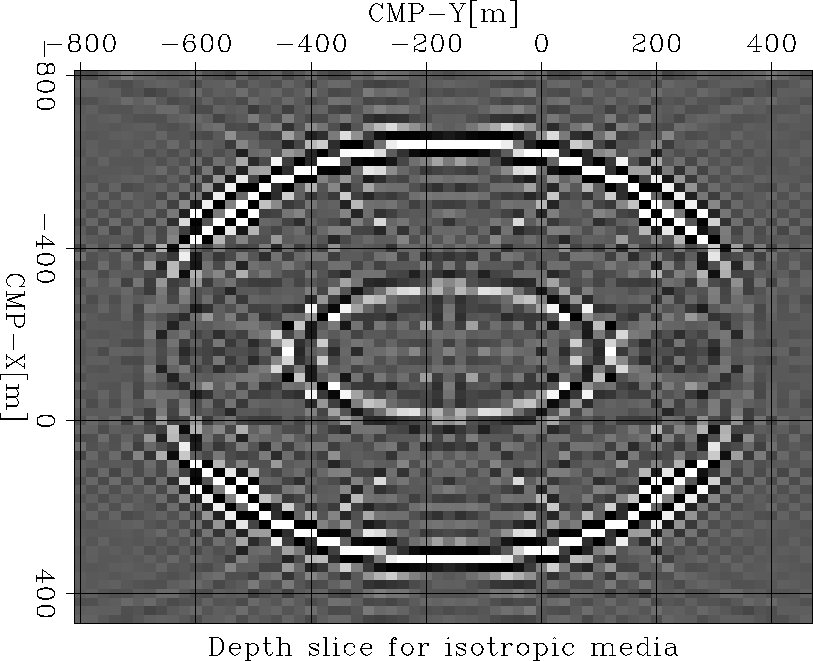
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) show depth slices of the 3-D impulse responses for elliptically anisotropic and isotropic media respectively. Again, we also observe significant differences between the two depth slices, especially the more elliptical nature of the depth slice for the anisotropic operator.
aniso15_inline
show depth slices of the 3-D impulse responses for elliptically anisotropic and isotropic media respectively. Again, we also observe significant differences between the two depth slices, especially the more elliptical nature of the depth slice for the anisotropic operator.
aniso15_inline
Figure 4 An inline slice of the 3D impulse response in an elliptically anisotropic media at y=0 m.




 iso_inline
iso_inline
Figure 5 An inline slice of the 3D impulse response in an isotropic media at y=0 m




 aniso15_xline
aniso15_xline
Figure 6 A cross-line slice of the 3D impulse response in an elliptically anisotropic media at x=0 m




 iso_xline
iso_xline
Figure 7 A cross-line slice of the 3D impulse response in an isotropic media at x=0 m




 aniso15_depth_slice
aniso15_depth_slice
Figure 8 A horizontal slice of the 3D impulse response in an elliptically anisotropic media at a depth of z=600 m.




 iso_depth_slice
iso_depth_slice
Figure 9 A horizontal slice of the 3D impulse response in an isotropic medium at z=600 m.










Next: Conclusion
Up: Sen and Biondi: COMAZ-AN
Previous: Error analysis
Stanford Exploration Project
5/3/2005
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) show in-line sections of the 3-D impulse responses for elliptically anisotropic and isotropic media respectively. These figures clearly show the difference of incorporating anisotropy into the Common Azimuth downward continuation operator, especially for energy propagating at moderate to steep angles.
Figures
show in-line sections of the 3-D impulse responses for elliptically anisotropic and isotropic media respectively. These figures clearly show the difference of incorporating anisotropy into the Common Azimuth downward continuation operator, especially for energy propagating at moderate to steep angles.
Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) show cross-line sections of the 3-D impulse responses for elliptically anisotropic and isotropic media respectively. Again it can be seen that there are significant differences for energy propagating at moderate to steep angles once anisotropy is incorporated into the Common Azimuth operator.
Finally, Figures
show cross-line sections of the 3-D impulse responses for elliptically anisotropic and isotropic media respectively. Again it can be seen that there are significant differences for energy propagating at moderate to steep angles once anisotropy is incorporated into the Common Azimuth operator.
Finally, Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) show depth slices of the 3-D impulse responses for elliptically anisotropic and isotropic media respectively. Again, we also observe significant differences between the two depth slices, especially the more elliptical nature of the depth slice for the anisotropic operator.
show depth slices of the 3-D impulse responses for elliptically anisotropic and isotropic media respectively. Again, we also observe significant differences between the two depth slices, especially the more elliptical nature of the depth slice for the anisotropic operator.