




Next: Estimation schemes based on
Up: CONDUCTIVITY: CANONICAL FUNCTIONS AND
Previous: CONDUCTIVITY: CANONICAL FUNCTIONS AND
Another topic of broad and continuing interest in the field of
composite materials is the study of heterogeneous conductors,
dielectrics, and -- for porous media -- fluid permeability
(Beran, 1968; Milton, 2002; Torquato, 2002).
Because of the wide range of
applications, including both thermal and electrical conduction,
and the theoretical interest in analysis of critical phenomena such as
percolation thresholds in resistor networks and localization
(Kirkpatrick, 1971; 1973),
this topic has surely been studied
as much or more than any other in the field of heterogeneous media.
Many results in this field of research can also be expressed in
terms of canonical functions. First define
| ![\begin{displaymath}
\Sigma(\sigma) \equiv \left[\sum_{i=1}^J \frac{v_i}{\sigma_i +
2\sigma}\right]^{-1} - 2\sigma,
\end{displaymath}](img102.gif) |
(28) |
where 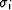 is the conductivity in the ith component, and
vi is the corresponding volume fraction, again having the
space filling constraint that
is the conductivity in the ith component, and
vi is the corresponding volume fraction, again having the
space filling constraint that 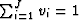 .Hashin-Shtrikman bounds (Hashin and Shtirkman, 1962)
on conductivity
for a multicomponent composite material can then be expressed as
.Hashin-Shtrikman bounds (Hashin and Shtirkman, 1962)
on conductivity
for a multicomponent composite material can then be expressed as
| 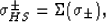 |
(29) |
where 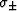 are the largest and smallest values of the
J isotropic conductivities present. These bounds are generally improvements
on the mean and harmonic mean bounds:
are the largest and smallest values of the
J isotropic conductivities present. These bounds are generally improvements
on the mean and harmonic mean bounds:
| ![\begin{displaymath}
\sigma_M = \sum_{i=1}^J v_i\sigma_i \qquad \hbox{and} \qquad
\sigma_H = \left[\sum_{i=1}^J \frac{v_i}{\sigma_i}\right]^{-1}.
\end{displaymath}](img106.gif) |
(30) |
Beran (1965; 1968) used variational methods to arrive at
improved bounds on conductivity for two-component media, again based
on information in spatial correlation functions. His results are
also expressible in terms of the canonical functions as
| 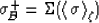 |
(31) |
and
| 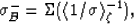 |
(32) |
where 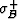 (
(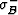 ) is the upper (lower) bound
and the
) is the upper (lower) bound
and the 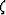 averages are the same ones we introduced here
previously [following Eq.(6)]. Since some of the
same measures of microstructure (in this case the
averages are the same ones we introduced here
previously [following Eq.(6)]. Since some of the
same measures of microstructure (in this case the 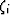 's)
can be used to bound both conductivity and elastic constants, it has
been noticed before that this fact and similar relations for other
systems can be used to produce various cross-property bounds
(Berryman and Milton, 1988; Gibiansky and Torquato, 1995),
thereby measuring one physical
property in order to bound another.
's)
can be used to bound both conductivity and elastic constants, it has
been noticed before that this fact and similar relations for other
systems can be used to produce various cross-property bounds
(Berryman and Milton, 1988; Gibiansky and Torquato, 1995),
thereby measuring one physical
property in order to bound another.





Next: Estimation schemes based on
Up: CONDUCTIVITY: CANONICAL FUNCTIONS AND
Previous: CONDUCTIVITY: CANONICAL FUNCTIONS AND
Stanford Exploration Project
5/3/2005
![\begin{displaymath}
\Sigma(\sigma) \equiv \left[\sum_{i=1}^J \frac{v_i}{\sigma_i +
2\sigma}\right]^{-1} - 2\sigma,
\end{displaymath}](img102.gif)
![\begin{displaymath}
\Sigma(\sigma) \equiv \left[\sum_{i=1}^J \frac{v_i}{\sigma_i +
2\sigma}\right]^{-1} - 2\sigma,
\end{displaymath}](img102.gif)
![\begin{displaymath}
\sigma_M = \sum_{i=1}^J v_i\sigma_i \qquad \hbox{and} \qquad
\sigma_H = \left[\sum_{i=1}^J \frac{v_i}{\sigma_i}\right]^{-1}.
\end{displaymath}](img106.gif)