




Next: Rigorous bounds
Up: CANONICAL FUNCTIONS AND THE
Previous: CANONICAL FUNCTIONS AND THE
To make progress towards our present goals, it will prove helpful
to take advantage of some observations made earlier about
both rigorous bounds and many of the known estimates for
moduli of elastic composites
(Berryman, 1982; 1995; Milton, 1987; 2002).
In particular,
it is known (Berryman, 1982) that if we introduce certain
functionals -- similar in analytical structure to Hill's formula
for the overall bulk modulus K*, which is
| ![\begin{displaymath}
K^*= \left[\sum_{i=1}^{J} \frac{v_i}{K_i+4\mu/3}\right]^{-1} - 4\mu/3,
\end{displaymath}](img1.gif) |
(1) |
valid when the shear modulus 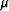 is a uniform constant
throughout the medium. Here Ki is the bulk modulus of the ith
constituent out of J constituents, and vi is the corresponding
volume fraction, with the constraint that
is a uniform constant
throughout the medium. Here Ki is the bulk modulus of the ith
constituent out of J constituents, and vi is the corresponding
volume fraction, with the constraint that 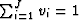 .This form is also similar to the form of the
Hashin-Shtrikman bounds (Hashin and Shtrikman, 1962; 1963)
for both bulk
and shear moduli -- many of the known formulas for composites
can be expressed simply in terms of these functionals.
Specifically, for analysis of effective bulk modulus K*, we introduce
.This form is also similar to the form of the
Hashin-Shtrikman bounds (Hashin and Shtrikman, 1962; 1963)
for both bulk
and shear moduli -- many of the known formulas for composites
can be expressed simply in terms of these functionals.
Specifically, for analysis of effective bulk modulus K*, we introduce
| ![\begin{displaymath}
\Lambda(\beta) \equiv \left[\sum_{i=1}^J
\frac{v_i}{K_i + \beta}\right]^{-1} - \beta,
\end{displaymath}](img4.gif) |
(2) |
while, for the effective shear modulus 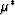 , we have
, we have
| ![\begin{displaymath}
\Gamma(\theta) \equiv \left[\sum_{i=1}^J
\frac{v_i}{\mu_i + \theta}\right]^{-1} - \theta.
\end{displaymath}](img6.gif) |
(3) |
Here 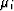 is the shear modulus of the ith
constituent out of J isotropic constituents.
The arguments
is the shear modulus of the ith
constituent out of J isotropic constituents.
The arguments 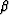 and
and 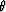 have dimensions of GPa,
and are always nonnegative.
Both functions increase monotonically as their arguments
increase. Furthermore, when the argument of each functional vanishes,
the result is the volume weighted harmonic mean (or Reuss average)
of the corresponding physical property. Similarly,
an analysis of the series expansion for each functional at large
arguments shows that, in the limit when the arguments go to infinity, the
functionals approach the volume weighted mean (or Voigt average)
of the corresponding physical property.
We call these expressions the ``canonical functions'' for elasticity,
as results expressible in these terms appear repeatedly in the
literature -- although published results are not necessarily
manipulated into these canonical forms by all authors.
The arguments
have dimensions of GPa,
and are always nonnegative.
Both functions increase monotonically as their arguments
increase. Furthermore, when the argument of each functional vanishes,
the result is the volume weighted harmonic mean (or Reuss average)
of the corresponding physical property. Similarly,
an analysis of the series expansion for each functional at large
arguments shows that, in the limit when the arguments go to infinity, the
functionals approach the volume weighted mean (or Voigt average)
of the corresponding physical property.
We call these expressions the ``canonical functions'' for elasticity,
as results expressible in these terms appear repeatedly in the
literature -- although published results are not necessarily
manipulated into these canonical forms by all authors.
The arguments 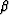 and
and 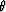 are called the ``transform parameters.''
are called the ``transform parameters.''
TABLE 1. Various bounds on bulk and shear modulus can be
expressed in terms of the canonical functions 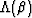 and
and
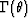 . Subscripts
. Subscripts  for
for  and
and 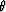 are for upper/lower (+/-) bounds. Subscripts
are for upper/lower (+/-) bounds. Subscripts 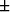 for the
elastic constants imply the highest/lowest (+/-)
values of the quantity present in the composite.
for the
elastic constants imply the highest/lowest (+/-)
values of the quantity present in the composite.
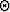 , X,
, X, 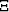 , and the averages
, and the averages 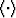 and
and
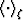 are all defined in the text.
are all defined in the text.
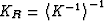 ,
,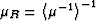 ,
,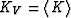 , and
, and 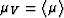 are the Reuss and Voigt averages of the respective moduli.
are the Reuss and Voigt averages of the respective moduli.
| 2.00
Bound |
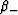 |
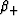 |
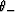 |
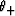 HS (HS, 1962; Walpole, 1969)
HS (HS, 1962; Walpole, 1969) |





Next: Rigorous bounds
Up: CANONICAL FUNCTIONS AND THE
Previous: CANONICAL FUNCTIONS AND THE
Stanford Exploration Project
5/3/2005
![\begin{displaymath}
K^*= \left[\sum_{i=1}^{J} \frac{v_i}{K_i+4\mu/3}\right]^{-1} - 4\mu/3,
\end{displaymath}](img1.gif)
![\begin{displaymath}
K^*= \left[\sum_{i=1}^{J} \frac{v_i}{K_i+4\mu/3}\right]^{-1} - 4\mu/3,
\end{displaymath}](img1.gif)
![\begin{displaymath}
\Lambda(\beta) \equiv \left[\sum_{i=1}^J
\frac{v_i}{K_i + \beta}\right]^{-1} - \beta,
\end{displaymath}](img4.gif)
![\begin{displaymath}
\Gamma(\theta) \equiv \left[\sum_{i=1}^J
\frac{v_i}{\mu_i + \theta}\right]^{-1} - \theta.
\end{displaymath}](img6.gif)
![]() and
and
![]() . Subscripts
. Subscripts ![]() for
for ![]() and
and ![]() are for upper/lower (+/-) bounds. Subscripts
are for upper/lower (+/-) bounds. Subscripts ![]() for the
elastic constants imply the highest/lowest (+/-)
values of the quantity present in the composite.
for the
elastic constants imply the highest/lowest (+/-)
values of the quantity present in the composite.
![]() , X,
, X, ![]() , and the averages
, and the averages ![]() and
and
![]() are all defined in the text.
are all defined in the text.
![]() ,
,![]() ,
,![]() , and
, and ![]() are the Reuss and Voigt averages of the respective moduli.
are the Reuss and Voigt averages of the respective moduli.