Generating Potential Functions

Generating orthogonal coordinate system meshes from PFs requires ascribing a physical interpretation to equipotentials: they are equivalent to extrapolation steps. Similarly, the characteristics of the PF gradient field are intrinsically related to geometric coordinate system rays. Figure  illustrates these concepts for the example of 2D wave-equation migration from topography.

 

topocoord Figure 1 Scenario of migration from topography. The upper and lower topographic surfaces are denoted 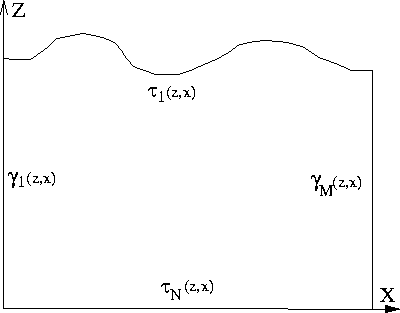$\tau_0 (z,x)$ and $\tau_N (z,x)$, respectively. Connecting vertical lines are denoted $\gamma_1(z,x)$ (left) and $\gamma_M(z,x)$ (right). The upper and lower surfaces have equipotential values of $\phi(\tau_0)=1$ and $\phi(\tau_N)=0$, respectively, whereas both side boundaries have zero normal derivatives.

This scenario requires extrapolating a wavefield comprised of M traces into the subsurface a total of N steps, which ideally occurs directly from the topographic surface. The upper boundary of the computational domain, denoted $\tau_0 (z,x)$ in this figure, is the acquisition surface. The lower boundary, denoted $\tau_N (z,x)$, is the desired flat subsurface datum. These two bounding surfaces are connected by two curves, $\gamma_1(z,x)$ and $\gamma_M(z,x)$, extending between the first and last extrapolation levels.

Solving for a PF satisfying Laplace's equation first requires specifying appropriate boundary conditions. Because distinct upper and lower equipotentials are desired, these two surfaces must have different constant values. Thus, I choose the following boundary conditions,  

$$\phi(\tau_0) = 1, \;\;\;\;\; \phi(\tau_N) = 0, \;\;\;\;\; ... ...{\partial \phi}{\partial {\bf n} }\right\vert _{\gamma_M} = 0,$$ (4)

where the derivative with respect to variable ${\bf n}$ is in the direction outward normal to the surface represented by $\gamma_1$ and $\gamma_M$.

The Laplace's equation defined by the boundary conditions in Equation (4) is representable by a system of equations similar those commonly solved with conjugate gradient methods Claerbout (1999),  

$${\bf W} {\bf L}{\bf m} \approx 0$$ (5)

subject to the following constraints,

$$\left( {\bf I}-{\bf W} \right) \left( {\bf m} -{\bf m}_{bnd}\right)=0,$$ (6)

where model vector ${\bf m}$ is the sought PF solution, ${\bf m}_{bnd}$ are the values on, and exterior to, the domain boundary, , ${\bf L}=\nabla^2$ is a Laplacian operator matrix, ${\bf W}$ is a mask operator indicating location of the boundary, and ${\bf I}$ is the identity operator.

I use the following algorithm to obtain PF solution, ${\bf m}$:

1.

Map the irregular topographic domain to a Cartesian mesh to generate vector ${\bf m}_{bnd}$;

2.

Fix the PF values on the boundary of, and external to, the mapped domain using the mask operator ${\bf W}$;

3.

Initialize the model vector with a starting guess (i.e., ${\bf m}_0$) exploiting the smooth variation of $\phi$ between the upper and lower surfaces (i.e., through linear interpolation of $\phi$ on [1,0] between $\tau_0(z_0,x_0)$ and $\tau_N(z_1,x_0)$);

4.

Solve system of equations in Equation (5) using a conjugate gradient algorithm Claerbout (1999), by allowing the solver to iterate until convergence is reached.

The resulting model vector, ${\bf m}$, is the desired potential function that can be input to the phase ray-tracing algorithm described below. Finally, as illustrated by the example below, this approach is directly applicable to 3D computational domains because conjugate gradient solvers still work in 3D after the geometry is unwrapped on to a helical coordinate system Claerbout (1999).