




Next: Numerical test examples
Up: Wang and Shan: Choosing
Previous: Self-adaptive Reference velocity choice
Gazdag and Sguazzero (1984) use the following method for merging the extrapolated wavefield. Assume that the two extrapolated wavefields with the different reference velocities vref1and vref2 are as follows:
| 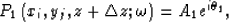 |
(18) |
| 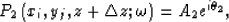 |
(19) |
where A1 and A2, and 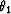 and
and 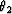 represent amplitude and phase, respectively. The merged wavefield at a spatial point is
represent amplitude and phase, respectively. The merged wavefield at a spatial point is
| 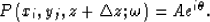 |
(20) |
The amplitude and phase of the merged wavefield is cauculated with
| 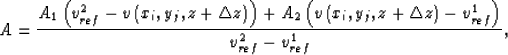 |
(21) |
and
| 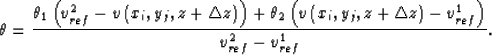 |
(22) |
where 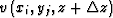 is the velocity at the spatial point
is the velocity at the spatial point 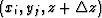 .
.Kessinger (1992) shows that the wavefield at a spatial point can be directly replaced by the extrapolated wavefield with the reference velocity corresponding to the spatial point. The following formula is used for merging the extrapolated wavefields with SSF operator
| ![\begin{eqnarray}
P\left( x_{i},y_{j},z+\triangle z;\omega \right) &=&
\delta \l...
...angle z}P\left( x_{i},y_{j},z+\triangle z;\omega \right)
\right],\end{eqnarray}](img43.gif) |
|
| (23) |
where
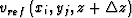 stands for the reference velocity at a spatial point
stands for the reference velocity at a spatial point 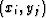 , vrefl
is the member of the set of chosen reference velocities with the index l. The delta function
, vrefl
is the member of the set of chosen reference velocities with the index l. The delta function 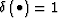 if
if 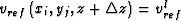 ; otherwise,
; otherwise, 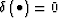 . With this method, the extrapolated wavefield can be directly inserted into the relevant position without storing it. However, the amplitude and phase of the merged wavefield is not so accurate in the case of severe lateral velocity variations.
We use quadratic interpolation to reconstruct the extrapolated wavefield with the following equation:
. With this method, the extrapolated wavefield can be directly inserted into the relevant position without storing it. However, the amplitude and phase of the merged wavefield is not so accurate in the case of severe lateral velocity variations.
We use quadratic interpolation to reconstruct the extrapolated wavefield with the following equation:
where 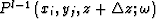 ,
, 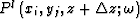 and
and 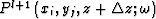 are the extrapolated wavefield at point
are the extrapolated wavefield at point 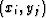 with the three adjacent reference velocities vrefl-1, vrefl and vrefl+1, respectively.
with the three adjacent reference velocities vrefl-1, vrefl and vrefl+1, respectively.





Next: Numerical test examples
Up: Wang and Shan: Choosing
Previous: Self-adaptive Reference velocity choice
Stanford Exploration Project
5/3/2005
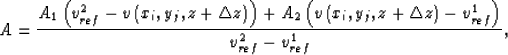
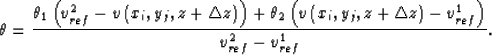
![\begin{eqnarray}
P\left( x_{i},y_{j},z+\triangle z;\omega \right) &=&
\delta \l...
...angle z}P\left( x_{i},y_{j},z+\triangle z;\omega \right)
\right],\end{eqnarray}](img43.gif)
![]() ,
, ![]() and
and ![]() are the extrapolated wavefield at point
are the extrapolated wavefield at point ![]() with the three adjacent reference velocities vrefl-1, vrefl and vrefl+1, respectively.
with the three adjacent reference velocities vrefl-1, vrefl and vrefl+1, respectively.