




Next: Conclusion
Up: Numerical example
Previous: A synthetic anisotropic dataset
Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -
-![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) compare the impulse responses of our algorithm with those of anisotropic
phase shift method.
The medium is a homogeneous, tilted TI medium.
The symmetry axis of the medium is in the (x,z) plane and is tilted
compare the impulse responses of our algorithm with those of anisotropic
phase shift method.
The medium is a homogeneous, tilted TI medium.
The symmetry axis of the medium is in the (x,z) plane and is tilted 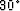 from the vertical direction.
The P-wave velocity in the direction parallel to the symmetry axis is 2000 m/s. The anisotropy parameters
from the vertical direction.
The P-wave velocity in the direction parallel to the symmetry axis is 2000 m/s. The anisotropy parameters
 and
and 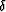 are 0.4 and 0.2, respectively. The location of the impulse is at x=2000 m and y=2000 m.
The travel time for the three impulses are 0.4 s, 0.6 s and 0.8 s, respectively.
Figure
are 0.4 and 0.2, respectively. The location of the impulse is at x=2000 m and y=2000 m.
The travel time for the three impulses are 0.4 s, 0.6 s and 0.8 s, respectively.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a depth slice of the impulse responses at z=1500 m.
Figure
shows a depth slice of the impulse responses at z=1500 m.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (a) is obtained with our algorithm
and Figure
(a) is obtained with our algorithm
and Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (b) is obtained with the anisotropic phase-shift method.
First, Figure
(b) is obtained with the anisotropic phase-shift method.
First, Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (a) is very similar to
(a) is very similar to ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (b). Second, the depth slice of the impulse response
is not a circle. The wave propagates faster in y than in x direction. Third, the impulse location
x=2000 m and y=2000 m is not the center of the impulse response. The impulse response is symmetric along y=2000m,
but it is not symmetric along x=2000 m.
filtercom
(b). Second, the depth slice of the impulse response
is not a circle. The wave propagates faster in y than in x direction. Third, the impulse location
x=2000 m and y=2000 m is not the center of the impulse response. The impulse response is symmetric along y=2000m,
but it is not symmetric along x=2000 m.
filtercom
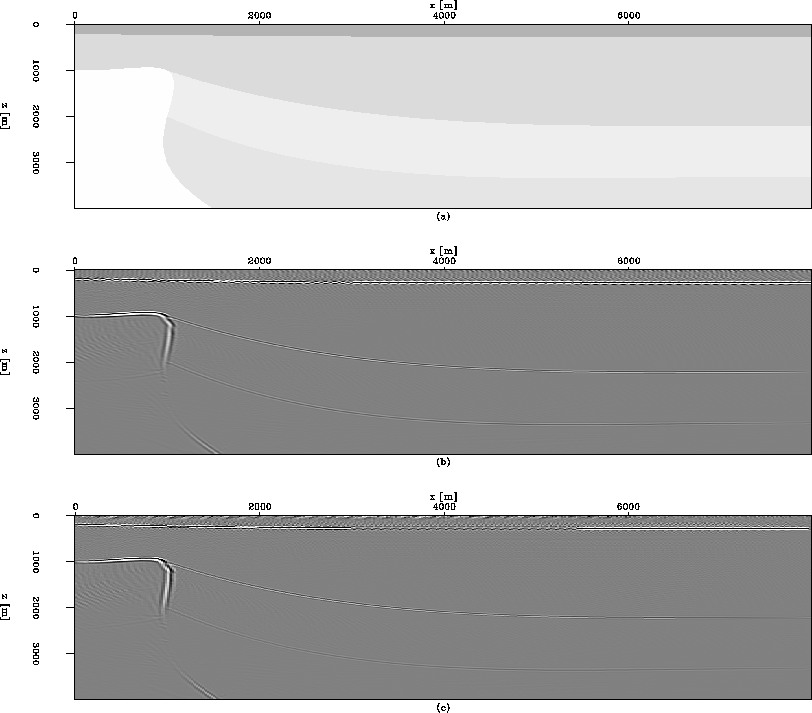
Figure 6 Comparison of the anisotropic plane-wave migration of a synthetic dataset by
the 19-point filter and the new 5-point filter. (a) The density model. (b) The migration result of the 19-point filter.
(c) The migration result of the new 5-point filter.





Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows an in-line slice of the impulse responses at y=2000 m.
Figure
shows an in-line slice of the impulse responses at y=2000 m.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (a) is obtained with our algorithm and Figure
(a) is obtained with our algorithm and Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (b) is obtained
with the anisotropic phase-shift method.
Figure
(b) is obtained
with the anisotropic phase-shift method.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a cross-line slice of the impulse responses at x=2000 m.
Figure
shows a cross-line slice of the impulse responses at x=2000 m.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (a) is obtained with our algorithm and Figure
(a) is obtained with our algorithm and Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (b) is obtained
with the anisotropic phase-shift method. From Figure
(b) is obtained
with the anisotropic phase-shift method. From Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , we can see that
the impulse of our algorithm is very close to that of the anisotropic phase-shift method at low-angle energy
and is different from the the anisotropic phase-shift method at high-angle energy. Since the medium is
homogeneous, the anisotropic phase-shift method is accurate. So our algorithm is accurate for the energy up
to
, we can see that
the impulse of our algorithm is very close to that of the anisotropic phase-shift method at low-angle energy
and is different from the the anisotropic phase-shift method at high-angle energy. Since the medium is
homogeneous, the anisotropic phase-shift method is accurate. So our algorithm is accurate for the energy up
to 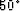 in the impulse response, compared to the anisotropic phase-shift method.
in the impulse response, compared to the anisotropic phase-shift method.





Next: Conclusion
Up: Numerical example
Previous: A synthetic anisotropic dataset
Stanford Exploration Project
5/3/2005
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -
-