




Next: Practical Implementation
Up: Alvarez and Artman: Wavefield
Previous: Overview of Mixed-domain Downward
The previous section suggests an alternative implementation of
mixed-domain migration. To see this more clearly, assume that, at each
depth step, we downward continue the wavefield with the true velocities
at that depth. In other words, compute 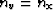 wavefields, each one
corresponding to the model velocity at each spatial location. No
split-step correction or higher-order approximation of kz would then
be required. The wavefield interpolation in
wavefields, each one
corresponding to the model velocity at each spatial location. No
split-step correction or higher-order approximation of kz would then
be required. The wavefield interpolation in  -
- domain
reduces to a simple selection of the appropriate wavefield, operation that
can be expressed as:
domain
reduces to a simple selection of the appropriate wavefield, operation that
can be expressed as:
| 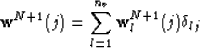 |
(2) |
where 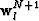 is the row of the array of wavefields extrapolated
with the velocity Vl, and
is the row of the array of wavefields extrapolated
with the velocity Vl, and 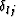 is the Kronecker delta that
selects from that row the corresponding j=l component. Notice that, since
we are extrapolating as many wavefields as there are spatial positions
(traces),
is the Kronecker delta that
selects from that row the corresponding j=l component. Notice that, since
we are extrapolating as many wavefields as there are spatial positions
(traces), 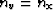 . Figure
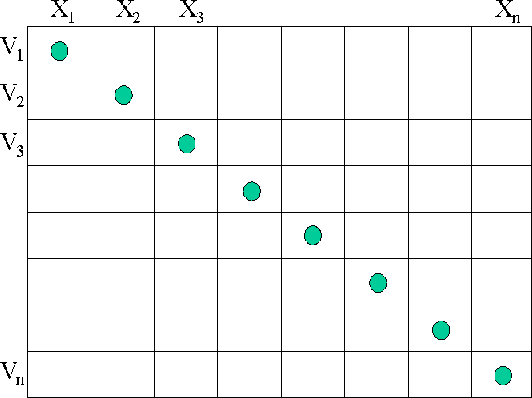
. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a schematic of the
velocity selection.
shows a schematic of the
velocity selection.
bin_vels1
Figure 1 Diagram illustrating velocity selection when there are
as many velocities as spatial locations.
|
|  |

In the 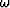 -
-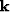 domain, Equation (2) becomes:
domain, Equation (2) becomes:
| 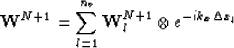 |
(3) |
where 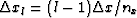 and we are using a single index to
represent the spatial axis in order to simplify the notation. The symbol
and we are using a single index to
represent the spatial axis in order to simplify the notation. The symbol
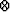 represents circular convolution.
represents circular convolution.
Notice that Equation (3) was derived without any approximation.
Let's make the computations more explicit in order to gain a better
appreciation for what it means:
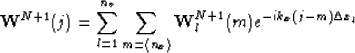
where 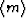 means that the summation is over the range nx
with modulus nx. That is,
means that the summation is over the range nx
with modulus nx. That is,
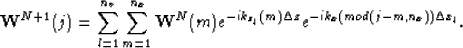
Let 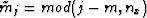 and exchange the order of summation:
and exchange the order of summation:
![\begin{displaymath}
\mathbf{W}^{N+1}(j)=\sum_{m=1}^{n_x}\mathbf{W}^N(m)\sum_{l=1}^{n_v}
e^{-i[k_{z_l}(m)\Delta z+k_x(\tilde{m}_j)]\Delta x_l}.\end{displaymath}](img26.gif)
This equation shows that in order to compute the jth component of the
extrapolated wavefield in the 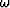 -
-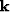 domain, we need to
take the dot product of the wavefield at the previous depth step with
a vector that contains all the velocity and interpolation information.
That is,
domain, we need to
take the dot product of the wavefield at the previous depth step with
a vector that contains all the velocity and interpolation information.
That is,
| 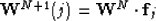 |
(4) |
where 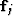 is the vector given by
is the vector given by
| ![\begin{displaymath}
\mathbf{f}_j=\sum_{l=1}^{n_v}e^{-i[k_{z_l}(m)\Delta z+k_x(\tilde{m}_j)]\Delta x_l}.\end{displaymath}](img29.gif) |
(5) |





Next: Practical Implementation
Up: Alvarez and Artman: Wavefield
Previous: Overview of Mixed-domain Downward
Stanford Exploration Project
5/3/2005
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a schematic of the
velocity selection.
shows a schematic of the
velocity selection.

![]() -
-![]() domain, Equation (2) becomes:
domain, Equation (2) becomes:
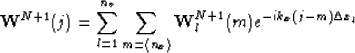
![]()
![]()