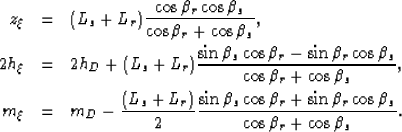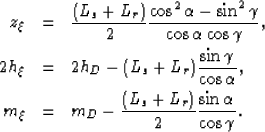Next: Tangent to the impulse
Up: Rosales and Biondi: PS-ADCIG
Previous: Conclusions and Future work
- Biondi, B., and Symes, W., 2004, Angle-domain common-image gathers for migration velocity analysis by wavefield-continuation imaging: Geophysics, 69, no. 5, 1283-1298.
-
- Biondi, B., 2005, Angle-domain common image gathers for anisotropic migration: SEP-120, 77-104.
-
- Brandsberg-Dahl, S., de Hoop, M. V., and Ursin, B., 1999, The sensitivity transform in the common scattering-angle/azimuth domain: 61st Ann. Internat. Mtg., Soc. Expl. Geophys., Expanded Abstracts, 1538-1541.
-
- de Bruin, C. G. M., Wapenaar, C. P. A., and Berkhout, A. J., 1990, Angle-dependent reflectivity by means of prestack migration: Geophysics, 55, no. 9, 1223-1234.
-
- Fomel, S., and Prucha, M., 1999, Angle-gather time migration: SEP-100, 141-150.
-
- Fomel, S., 1996, Migration and velocity analysis by velocity continuation: SEP-92, 159-188.
-
- Prucha, M., Biondi, B., and Symes, W., 1999, Angle-domain common-image gathers by wave-equation migration: 69th Ann. Internat. Meeting, Soc. of Expl. Geophys., Expanded Abstracts, 824-827.
-
- Rickett, J., and Sava, P., 2002, Offset and angle-domain common image-point gathers for shot-profile migration: Geophysics, 67, 883-889.
-
- Rosales, D., and Rickett, J., 2001a, ps-wave polarity reversal in angle domain common-image
gathers: SEP-108, 35-44.
-
- Rosales, D., and Rickett, J., 2001b, PS-wave polarity reversal in angle domain common-image gathers: 71st Annual Internat. Mtg., Expanded Abstracts, 1843-1846.
-
- Sava, P., and Fomel, S., 2000, Angle-gathers by Fourier Transform: SEP-103, 119-130.
-
- Sava, P., and Fomel, S., 2003, Angle-domain common-image gathers by wavefield continuation methods: Geophysics, 68, no. 3, 1065-1074.
-
A
In this part, we obtain the relation to transform subsurface offset-domain
common-image gathers into angle-domain common-image gathers for the
case of PS data.
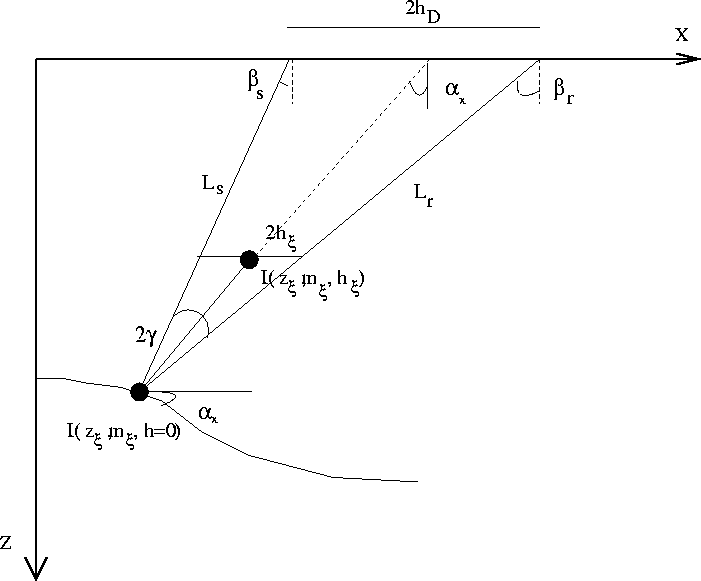
To perform this derivation, we use the geometry in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) in order to obtain the parametric equations for migration on a constant
velocity medium.
in order to obtain the parametric equations for migration on a constant
velocity medium.
Following the derivation of Fomel (1996) and
Fomel and Prucha (1999),
and applying simple trigonometry and geometry to Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
we obtain parametric equations for migrating an impulse recorded at time tD,
midpoint mD and surface offset hD as follows:
,
we obtain parametric equations for migrating an impulse recorded at time tD,
midpoint mD and surface offset hD as follows:
angles2
Figure 9 Parametric formulation of the
impulse response.
|
|  |

| 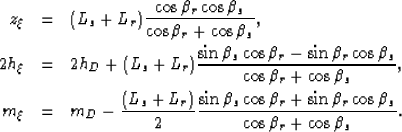 |
|
| |
| (14) |
where the total path length is:
| 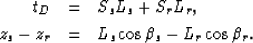 |
|
| (15) |
From that system of equations, Biondi (2005) shows that the total path length is
| 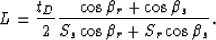 |
(16) |
Appendix A shows that we can rewrite system (14) as:
| 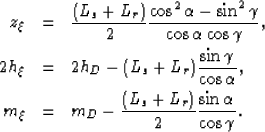 |
|
| |
| (17) |
where  and
and 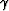 follow the same definition as in equation (3).
where,
L in terms of the angles
follow the same definition as in equation (3).
where,
L in terms of the angles  and
and 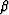 is:
is:
| 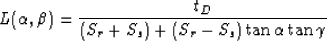 |
(18) |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) in order to obtain the parametric equations for migration on a constant
velocity medium.
in order to obtain the parametric equations for migration on a constant
velocity medium.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) in order to obtain the parametric equations for migration on a constant
velocity medium.
in order to obtain the parametric equations for migration on a constant
velocity medium.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
we obtain parametric equations for migrating an impulse recorded at time tD,
midpoint mD and surface offset hD as follows:
,
we obtain parametric equations for migrating an impulse recorded at time tD,
midpoint mD and surface offset hD as follows: