 |
Figure 3 Both solutions for
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) presents such result. The right panel presents the positive solution surface,
the left panel presents the negative one.
The positive solution is more stable than the negative solution. Note
that the solution for the quadratic system (7) is singular when
presents such result. The right panel presents the positive solution surface,
the left panel presents the negative one.
The positive solution is more stable than the negative solution. Note
that the solution for the quadratic system (7) is singular when  |
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the first of equations (4),
that is the expression for the full-aperture angle as a function of
shows the first of equations (4),
that is the expression for the full-aperture angle as a function of ![]() and
the velocity ratio,
and
the velocity ratio, ![]() . Remember that for the converted-mode case,
. Remember that for the converted-mode case,
![]() is related to the geologic dip (equation (12), but it's not the
dip itself. In order to understand better the previous plot, we take a look at
Figure
is related to the geologic dip (equation (12), but it's not the
dip itself. In order to understand better the previous plot, we take a look at
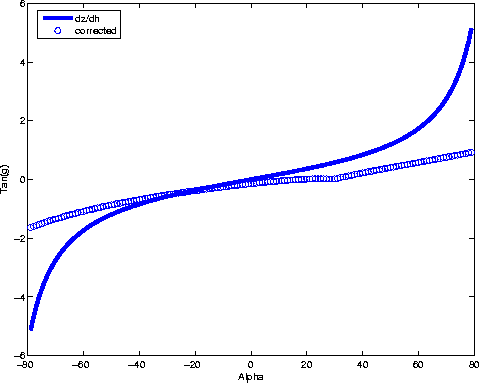
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . This figure is a cut along
. This figure is a cut along ![]() on
Figure
on
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (dotted line) and it's compared against the
conventional approach, which is
(dotted line) and it's compared against the
conventional approach, which is ![]() equals the partial derivative of depth with
respect to offset. If we omit the contribution of
equals the partial derivative of depth with
respect to offset. If we omit the contribution of ![]() and
and
![]() , we introduce a considerable error in the transformation from
SODCIGs into ADCIGs for the converted-mode case.
, we introduce a considerable error in the transformation from
SODCIGs into ADCIGs for the converted-mode case.
|
ang_cwv_alpha
Figure 4 Full-aperture angle ( | 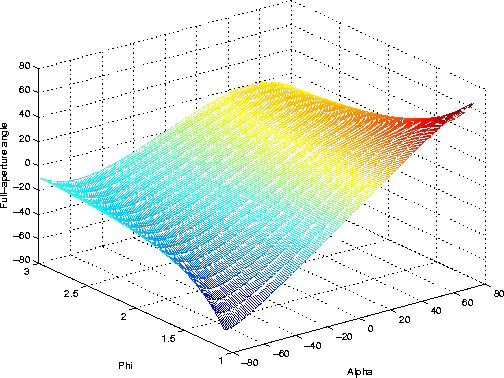 |
|
ang_cwv_diff
Figure 5 Difference between the conventional approach for ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . .
|  |
The first of equations (4) establishes a relationship between ![]() and the partial derivative of depth with respect to offset. We derive this relation
following a wave-equation approach. Appendix A shows that we can arrive at the same
conclusion following an integral summation approach.
Figure
and the partial derivative of depth with respect to offset. We derive this relation
following a wave-equation approach. Appendix A shows that we can arrive at the same
conclusion following an integral summation approach.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) summarizes both approaches. This figure presents
two surfaces, both of them correspond to
summarizes both approaches. This figure presents
two surfaces, both of them correspond to ![]() . The color
surface represents the computation with the integral summation approach (Appendix B);
and the black surface represents the computation with the wave-equation approach
(equation (4)). Both surfaces have a perfect match, this strongly suggests
that equations (4) is accurate, and must be followed for an appropriate
transformation from SODCIGs into ADCIGs for converted-mode seismic.
. The color
surface represents the computation with the integral summation approach (Appendix B);
and the black surface represents the computation with the wave-equation approach
(equation (4)). Both surfaces have a perfect match, this strongly suggests
that equations (4) is accurate, and must be followed for an appropriate
transformation from SODCIGs into ADCIGs for converted-mode seismic.
|
ang_cwv_wei_surf_comp
Figure 6 Wave-equation approach compared with Integral summation approach. Both of them arrive to the same surface. | 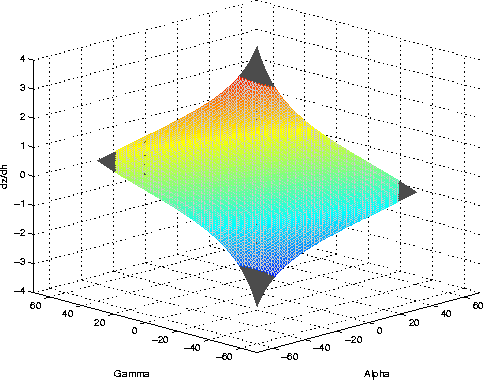 |