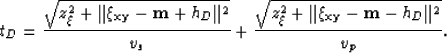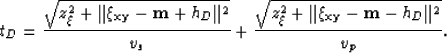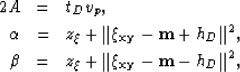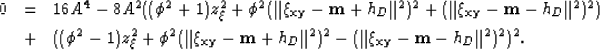Next: REFERENCES
Up: Rosales and Biondi: PS-COMAZ
Previous: Impulse response
We presented the converted-mode PS 3-D common-azimuth
migration operator. The difference between
this operator and the single-mode PP
operator is the use of two different velocity fields.
Therefore, a more careful implementation is needed
to ensure the correct velocity model.
We demonstrate that the subsurface area covered by the
PS common-azimuth migration operator is different than that
covered by the PP common-azimuth
migration operator; therefore, only the area that the two surfaces
share can be used for rock-properties analysis based on the
two complementary images. This might have important impacts
on the reservoir-characterization process.
A
This section derives
the exact solution for the common azimuth prestack migration for a
reflecting point within an homogeneous Earth.
The total travel time is
| 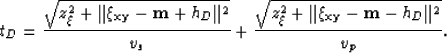 |
(8) |
The following procedure shows how to go from
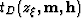 to
to 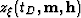 :
:
| 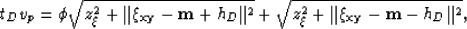 |
(9) |
where 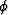 represents the P-to-S velocities ratio.
If we make the following definitions,
represents the P-to-S velocities ratio.
If we make the following definitions,
| 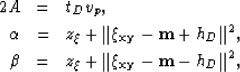 |
|
| |
| (10) |
(9) becomes
| 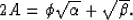 |
(11) |
We square both sides to get a new equation with only one square root:
| 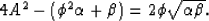 |
(12) |
Squaring again to eliminate the square root, and combining elements, we obtain
| 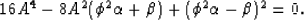 |
(13) |
This expression is a 4th degree polynomial in 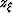 ; which is:
; which is:
| 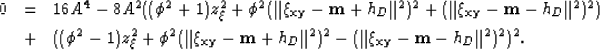 |
|
| (14) |
This can also be writen as follows
| 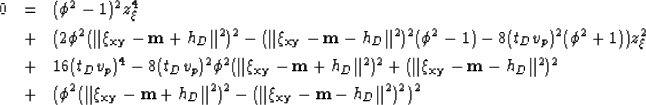 |
|
| |
| |
| (15) |
This polynomial equation has 4 solutions, which take the following well known form:
| 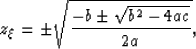 |
(16) |
where
| 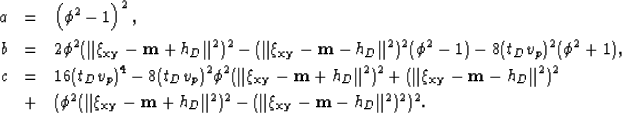 |
|
| |
| |
| (17) |





Next: REFERENCES
Up: Rosales and Biondi: PS-COMAZ
Previous: Impulse response
Stanford Exploration Project
5/3/2005