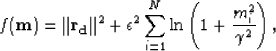
In this paper, we use the method of Sacchi and Ulrych (1995) to estimate a sparse model m. This technique imposes a Cauchy form probability-density function to the model parameters. This long-tailed probability-density function isolates the most energetic components of the radon domain and ignores the smallest, thus giving a minimum entropy solution. Note that other techniques such as stochastic inversion Thorson and Claerbout (1985) are also available.
To obtain a sparse radon domain m, a regularization term, i.e., the Cauchy function, is introduced in equation (7) as follows:
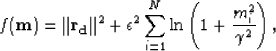 |
(8) |
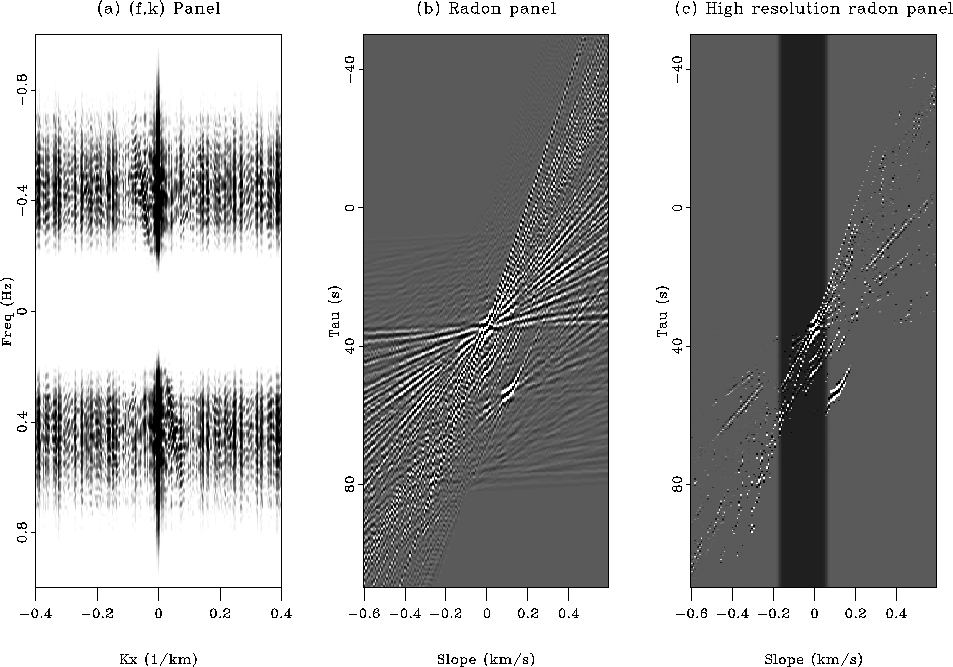
To demonstrate the effectiveness of the sparse radon transform for signal noise separation, we show the representation of the data panel from Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) in the f-k domain (a), the radon domain (b), and the sparse radon domain (c). Much of the energy in the synthetic data panel follows linear moveout. Therefore, the dominant factor in real data for signal/noise separation becomes the moveout of the scattered arrival compared to the direct arrival. f-k filtering is effective at isolating energy with differing dips with proper spatial sampling but is unable to isolate the energy in time regardless of sampling geometry. The side reflection and the direct arrival are colocated in f-k space and can not be separated. In the radon domain, the side reflection and the direct arrivals map to distinctly different dips for different
in the f-k domain (a), the radon domain (b), and the sparse radon domain (c). Much of the energy in the synthetic data panel follows linear moveout. Therefore, the dominant factor in real data for signal/noise separation becomes the moveout of the scattered arrival compared to the direct arrival. f-k filtering is effective at isolating energy with differing dips with proper spatial sampling but is unable to isolate the energy in time regardless of sampling geometry. The side reflection and the direct arrival are colocated in f-k space and can not be separated. In the radon domain, the side reflection and the direct arrivals map to distinctly different dips for different ![]() 's. But, without sparseness constraints many spurious artifacts are introduced from unwanted arrivals. The shaded region near zero slope represents an example radon mute that would remove the side reflection without reducing energy following the moveout of the direct arrival.
's. But, without sparseness constraints many spurious artifacts are introduced from unwanted arrivals. The shaded region near zero slope represents an example radon mute that would remove the side reflection without reducing energy following the moveout of the direct arrival.
 |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) in the f-k domain (a), the radon domain (b), and the sparse linear radon domain (c). The letters denote arrival location identified in Figure
in the f-k domain (a), the radon domain (b), and the sparse linear radon domain (c). The letters denote arrival location identified in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The f-k domain allows the isolation of distinct dips but does not offer a way to isolate different dips in time (e.g. time variable dip filter). The standard linear radon domain offers the possibility of separating dips as a function of time but introduces artifacts related to the transform. The sparse linear radon transform (c) allows us to isolate energy in time as in (b) while minimizing artifacts introduced from the transform. The shaded region indicates the radon mute used for the synthetic example shown in Figure
. The f-k domain allows the isolation of distinct dips but does not offer a way to isolate different dips in time (e.g. time variable dip filter). The standard linear radon domain offers the possibility of separating dips as a function of time but introduces artifacts related to the transform. The sparse linear radon transform (c) allows us to isolate energy in time as in (b) while minimizing artifacts introduced from the transform. The shaded region indicates the radon mute used for the synthetic example shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.