




Next: Anti-aliasing implications
Up: Artman and Fomel: Fourier
Previous: Theory
To test the above algorithm, synthetic data was generated and migrated
with both the conventional space-domain and Fourier-domain imaging
conditions. Images were created by migrating a single shot produced over a
single reflecting layer within a constant velocity medium. The
location, x, and offset, h, axes had the same extent and sampling.
This is true for both implementations of the imaging condition.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the comparison of the space-domain
impulse response to the Fourier equivalent developed above for the
zero dip reflector. Both seem to provide identical
results when viewed at subsurface offset h=0 at
the x-z plane. The smile shapes are due to the limited extent of
the acquisition along the surface. However, Figure
shows the comparison of the space-domain
impulse response to the Fourier equivalent developed above for the
zero dip reflector. Both seem to provide identical
results when viewed at subsurface offset h=0 at
the x-z plane. The smile shapes are due to the limited extent of
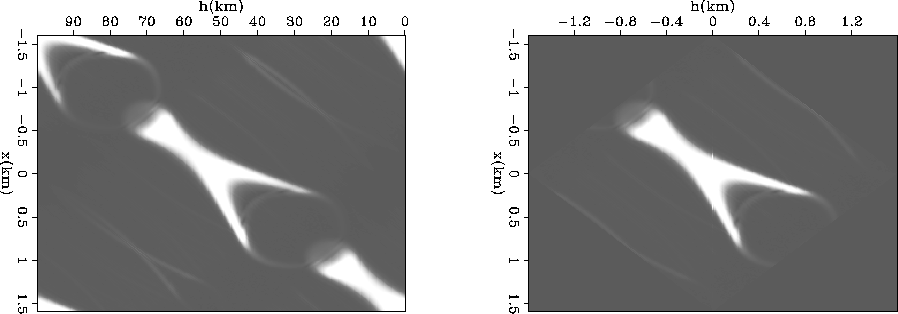
the acquisition along the surface. However, Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) compares the algorithms across the x-h plane at the depth of a
correctly migrated image point. While at zero offset the two images
are the same, the Fourier-domain implementation has obvious
replications at the end of the dog-bone shaped energy distribution.
Aliased energy is also introduced into the upper-right and lower-left
corners of the image space. This periodicity is not encountered with
the space-domain implementation.
compares the algorithms across the x-h plane at the depth of a
correctly migrated image point. While at zero offset the two images
are the same, the Fourier-domain implementation has obvious
replications at the end of the dog-bone shaped energy distribution.
Aliased energy is also introduced into the upper-right and lower-left
corners of the image space. This periodicity is not encountered with
the space-domain implementation.
imp
Figure 1 Migration impulse response
through a constant velocity medium of both space-domain and Fourier
domain implementation of the shot-profile imaging condition viewed
at h=0 on the x-z image plane.
|
|  |





imp-comp
Figure 2 Migration impulse response
through a constant velocity medium of both space-domain and Fourier
domain implementation of the shot-profile imaging condition viewed
at the depth of a focused image point on the x-h image plane.
|
|  |





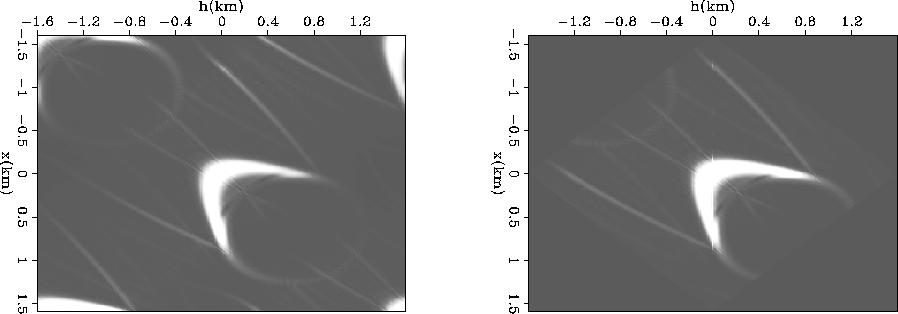
By adding dip to the reflection point, the dog-bone shape in the x-h
plane becomes skewed. Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) are produced with a reflector with 20o and
40o dip respectively. While the zero-offset image of the x-z
plane remains the same, the periodicity of the Fourier-domain algorithm is
again visible as compared to the computation of the imaging condition
in the space-domain. Notice that as dip increases, the saddle point
of the dog-bone has moved away from zero offset and the image gives
the sense of tipping into the page.
are produced with a reflector with 20o and
40o dip respectively. While the zero-offset image of the x-z
plane remains the same, the periodicity of the Fourier-domain algorithm is
again visible as compared to the computation of the imaging condition
in the space-domain. Notice that as dip increases, the saddle point
of the dog-bone has moved away from zero offset and the image gives
the sense of tipping into the page.
imp-dip-comp
Figure 3 20o dip reflector
image comparison. Left is Fourier-domain implementation. Right is
space-domain implementation. Image is extracted at the depth of a
focused image point on the x-h image plane.
|
|  |





imp-dip-2-comp
Figure 4 40o dip reflector
image comparison. Left is Fourier-domain implementation. Right is
space-domain implementation. Image is extracted at the depth of a
focused image point on the x-h image plane.
|
|  |





The onset of the replications are at precisely half the offset and
surface location axes. To remove this type of artifact in the Fourier
domain, interpolation of both axes by a factor of two would be
required. From equation 7, we note that the wavefields have
already required a factor of two interpolation to facilitate the
algorithm. Interpolating the image by a factor of two again
substantially increases memory consumption and computational effort
for this implementation.
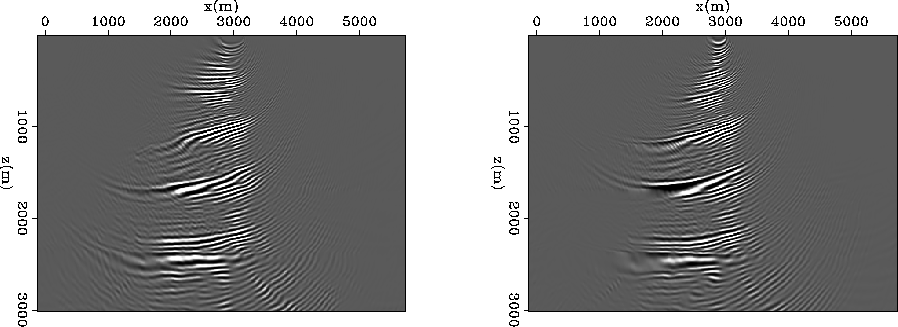
The first shot from the Marmousi synthetic data was migrated to
examine the effects of the above periodicity injected into the image
using the Fourier-domain imaging condition. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) compares the image from the first shot in the data computed with both
space-domain and Fourier-domain imaging conditions. At great depth,
the images are largely comparable, while at less than 1000 meters, the
images are completely different. This is due to the combined effects
of periodicity of the Fourier computed image and the steep dips of the model.
compares the image from the first shot in the data computed with both
space-domain and Fourier-domain imaging conditions. At great depth,
the images are largely comparable, while at less than 1000 meters, the
images are completely different. This is due to the combined effects
of periodicity of the Fourier computed image and the steep dips of the model.
marm.new
Figure 5 Images from the first shot in
the Marmousi data set. Left panel computed with the Fourier-domain
imaging condition, and the right panel with the conventional space
domain algorithm.
|
|  |





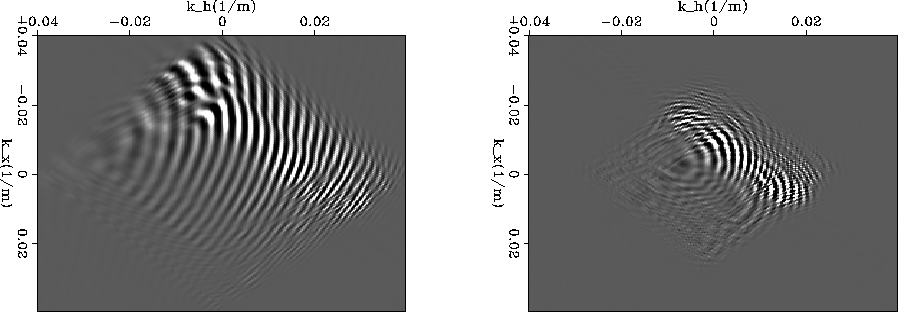
Deeper in the section, the problem is less apparent and the Fourier
domain imaging condition is much closer to the space-domain result.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) demonstrates how the zeroing of the evanescent
waves through the course of the migration effectively limits the range
of wavenumber energy allowed into the image. After the evanescent
limitations are more restrictive than the effects of the Fourier
domain periodicity, the artifacts begin to diminish.
demonstrates how the zeroing of the evanescent
waves through the course of the migration effectively limits the range
of wavenumber energy allowed into the image. After the evanescent
limitations are more restrictive than the effects of the Fourier
domain periodicity, the artifacts begin to diminish.
dslice
Figure 6 Images from the first shot in
the Marmousi data set. Depth slices, computed with the Fourier
domain imaging condition, are extracted from z=250m and z=1188m.
|
|  |





However, the images for a complex medium are definitely not strictly
equivalent for the two alternative imaging condition implementations.
By interpolating the kx and kh axes, it is possible to remove
the limitation imposed by the periodicity at the memory/disk cost of
4nx2 per depth level.





Next: Anti-aliasing implications
Up: Artman and Fomel: Fourier
Previous: Theory
Stanford Exploration Project
5/3/2005
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the comparison of the space-domain
impulse response to the Fourier equivalent developed above for the
zero dip reflector. Both seem to provide identical
results when viewed at subsurface offset h=0 at
the x-z plane. The smile shapes are due to the limited extent of
the acquisition along the surface. However, Figure
shows the comparison of the space-domain
impulse response to the Fourier equivalent developed above for the
zero dip reflector. Both seem to provide identical
results when viewed at subsurface offset h=0 at
the x-z plane. The smile shapes are due to the limited extent of
the acquisition along the surface. However, Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) compares the algorithms across the x-h plane at the depth of a
correctly migrated image point. While at zero offset the two images
are the same, the Fourier-domain implementation has obvious
replications at the end of the dog-bone shaped energy distribution.
Aliased energy is also introduced into the upper-right and lower-left
corners of the image space. This periodicity is not encountered with
the space-domain implementation.
compares the algorithms across the x-h plane at the depth of a
correctly migrated image point. While at zero offset the two images
are the same, the Fourier-domain implementation has obvious
replications at the end of the dog-bone shaped energy distribution.
Aliased energy is also introduced into the upper-right and lower-left
corners of the image space. This periodicity is not encountered with
the space-domain implementation.





