




Next: Implementation
Up: R. Clapp: Regularization
Previous: Results
There is a notable drawback from the approach
described above.
The operator 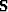 can be quite
costly, We are
doing nx*ny AMO transforms
for every output (hx,hy). If
we are only interested in a
common azimuth dataset
can be quite
costly, We are
doing nx*ny AMO transforms
for every output (hx,hy). If
we are only interested in a
common azimuth dataset 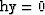 , the cost
is acceptable as long as ny is
fairly small.
If we want any cross
line offset output
offset the cost isn't acceptable.
In addition
, the cost
is acceptable as long as ny is
fairly small.
If we want any cross
line offset output
offset the cost isn't acceptable.
In addition 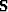 is a modified version (because
of the AMO transform) of a small 2-D box
car filter. If you desire additional smoothness
in the in-line offset direction (to
suppress amplitude variations) we must try
a different approach.
is a modified version (because
of the AMO transform) of a small 2-D box
car filter. If you desire additional smoothness
in the in-line offset direction (to
suppress amplitude variations) we must try
a different approach.
Biondi and Vlad (2001) proposed
reducing the dimensionality of the problem
by ignoring the azimuth direction. They
added a smoothness constraint to the
problem by applying a Leaky derivative 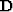 operator between AMO transformed (t,cmpx,cmpy)
cubes setting up the minimization,
operator between AMO transformed (t,cmpx,cmpy)
cubes setting up the minimization,
| 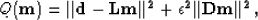 |
(7) |
where  controls the weighting between the two goals.
They preconditioned the problem with the inverse of
controls the weighting between the two goals.
They preconditioned the problem with the inverse of 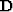 ,leaky integration between AMO transformed cubes
,leaky integration between AMO transformed cubes 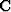 and
applied the same Hessian approximation to obtain the
approximation
and
applied the same Hessian approximation to obtain the
approximation
| 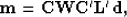 |
(8) |
where 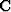 is the inverse of
is the inverse of 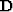 and
and
| ![\begin{displaymath}
\bf W^{-1} = {\rm diag} \left[ \bf C' \bf L' \bf L\bf C {\bf 1} +\epsilon^2 \right] .\end{displaymath}](img34.gif) |
(9) |
Clapp (2003b) noted
that ignoring the azimuth removed some of the advantage of
using the AMO operator and suggested that
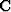 should be applying polynomial division
with a 2-D filter operating in the the (hx,hy) plane.
For this exercise I chose a small helical derivative
for my 2-D filter Claerbout (1999).
should be applying polynomial division
with a 2-D filter operating in the the (hx,hy) plane.
For this exercise I chose a small helical derivative
for my 2-D filter Claerbout (1999).
![]() operator between AMO transformed (t,cmpx,cmpy)
cubes setting up the minimization,
operator between AMO transformed (t,cmpx,cmpy)
cubes setting up the minimization,